
La proiezione ortogonale di un punto su un piano è un concetto fondamentale in geometria descrittiva e, più in generale, in matematica e ingegneria. Essa rappresenta la base per la rappresentazione bidimensionale di oggetti tridimensionali, trovando applicazione in diversi ambiti, dall'architettura al design industriale. Comprendere a fondo questo principio è essenziale per visualizzare e manipolare oggetti nello spazio.
Cos'è la Proiezione Ortogonale?
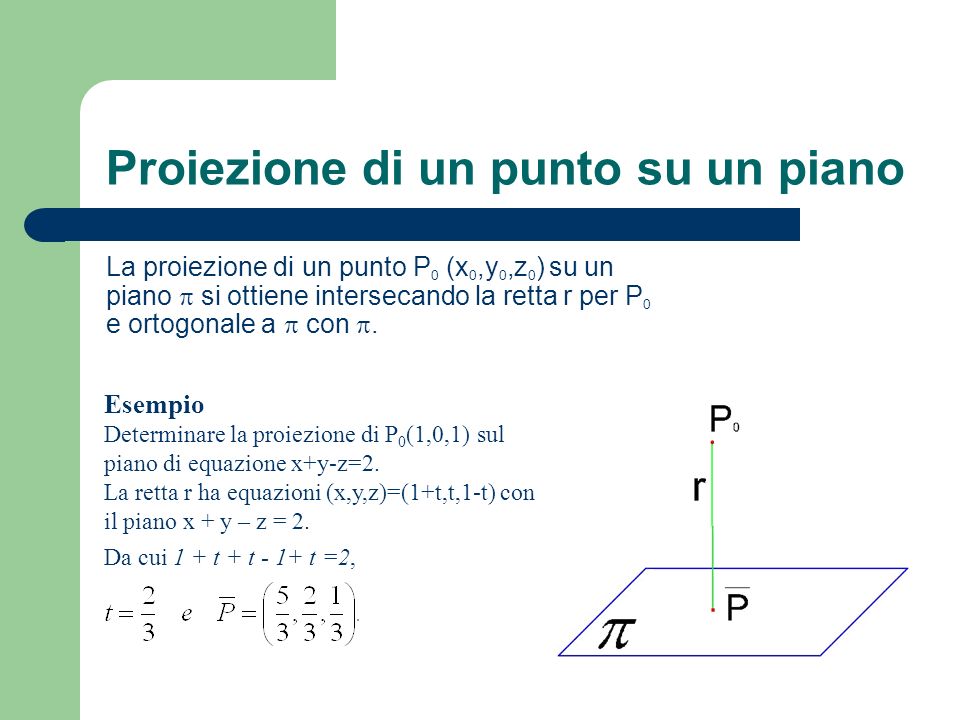
In termini semplici, la proiezione ortogonale di un punto P su un piano π è il punto P' sul piano π ottenuto tracciando una retta perpendicolare (ortogonale) dal punto P al piano π. Il punto di intersezione tra questa retta e il piano è il punto proiettato P'. È importante sottolineare che la proiezione ortogonale preserva le relazioni geometriche (rette parallele rimangono parallele) ma altera le lunghezze e gli angoli, salvo quelli tra rette parallele al piano di proiezione.
Elementi Chiave
- Punto: L'elemento che viene proiettato.
- Piano di Proiezione: La superficie su cui il punto viene proiettato.
- Retta di Proiezione (Proiettante): La retta perpendicolare al piano di proiezione che passa per il punto.
- Proiezione: Il punto di intersezione tra la retta di proiezione e il piano di proiezione.
Come Determinare la Proiezione Ortogonale
La determinazione della proiezione ortogonale può essere eseguita in diversi modi, a seconda delle informazioni disponibili. Analizziamo alcuni approcci:
Metodo Geometrico
Questo metodo è concettualmente il più semplice. Richiede di visualizzare (o disegnare) una retta perpendicolare al piano passante per il punto. L'intersezione tra questa retta e il piano fornisce la proiezione. In pratica, questo metodo è limitato a situazioni semplici o a rappresentazioni grafiche accurate.
Metodo Analitico
Questo metodo utilizza l'algebra lineare e la geometria analitica per determinare la proiezione. Richiede di conoscere le equazioni del piano e le coordinate del punto. Ecco i passaggi fondamentali:

- Equazione del Piano: Il piano π è definito da un'equazione del tipo ax + by + cz + d = 0, dove (a, b, c) è il vettore normale al piano.
- Equazione della Retta Proiettante: La retta passante per il punto P(x0, y0, z0) e perpendicolare al piano π ha equazione parametrica:
- x = x0 + at
- y = y0 + bt
- z = z0 + ct
- Intersezione Retta-Piano: Sostituire le equazioni parametriche della retta nell'equazione del piano per trovare il valore di t corrispondente all'intersezione: a(x0 + at) + b(y0 + bt) + c(z0 + ct) + d = 0 Risolvendo per t, otteniamo: t = -(ax0 + by0 + cz0 + d) / (a2 + b2 + c2)
- Coordinate del Punto Proiettato: Sostituire il valore di t trovato nelle equazioni parametriche della retta per ottenere le coordinate del punto proiettato P'(x', y', z'):
- x' = x0 + at
- y' = y0 + bt
- z' = z0 + ct
Questo metodo è preciso e può essere implementato facilmente in software di calcolo.
Utilizzo di Matrici di Proiezione
In grafica 3D e in applicazioni di computer vision, si utilizzano spesso matrici di proiezione per trasformare le coordinate dei punti nello spazio 3D in coordinate 2D. La matrice di proiezione ortogonale mappa i punti 3D su un piano 2D, mantenendo le proprietà di parallelismo. La costruzione della matrice dipende dall'orientamento del piano di proiezione e dalla posizione della telecamera virtuale.
Esempi Pratici e Applicazioni
La proiezione ortogonale trova un'ampia gamma di applicazioni in diversi settori:
- Architettura e Ingegneria Civile: I disegni tecnici di edifici e strutture sono spesso realizzati utilizzando proiezioni ortogonali (piante, prospetti, sezioni) per rappresentare accuratamente le dimensioni e le relazioni spaziali degli elementi costruttivi. Le planimetrie, ad esempio, sono proiezioni ortogonali del fabbricato su un piano orizzontale.
- Design Industriale: Nella progettazione di prodotti, le proiezioni ortogonali sono utilizzate per creare disegni dettagliati che specificano le dimensioni, le forme e le tolleranze dei componenti. Questi disegni sono essenziali per la fabbricazione e l'assemblaggio.
- Cartografia: Le mappe topografiche utilizzano proiezioni ortogonali per rappresentare la superficie terrestre su un piano. Sebbene le mappe reali utilizzino proiezioni più complesse per minimizzare la distorsione, il principio base rimane quello della proiezione ortogonale (almeno localmente).
- Grafica Computerizzata: Le proiezioni ortogonali (isometrica, dimetrica, trimetrica) sono utilizzate in giochi e applicazioni CAD per creare immagini che preservano le proporzioni degli oggetti, pur apparendo tridimensionali. Pensiamo ai giochi di strategia a turni che offrono una visuale dall'alto.
- Medicina: Le immagini radiografiche e le scansioni TC possono essere considerate come proiezioni di densità di tessuti su un piano. Sebbene non siano proiezioni ortogonali perfette, il concetto di proiezione è fondamentale per l'interpretazione di queste immagini.
Ad esempio, in architettura, un architetto potrebbe avere bisogno di proiettare ortogonalmente una finestra su una parete per calcolare l'area della finestra e quindi determinare la quantità di luce che entrerà nella stanza. Oppure, un ingegnere potrebbe usare le proiezioni ortogonali per disegnare un pezzo meccanico, garantendo che tutte le dimensioni siano corrette e che il pezzo si adatti correttamente nell'assemblaggio finale.
Limitazioni e Considerazioni
Sebbene la proiezione ortogonale sia uno strumento potente, è importante considerare le sue limitazioni:

- Perdita di Profondità: La proiezione ortogonale appiattisce l'oggetto lungo la direzione di proiezione, perdendo quindi informazioni sulla profondità. Questo può rendere difficile percepire la forma tridimensionale dell'oggetto da una singola proiezione.
- Distorsione delle Lunghezze: Le lunghezze delle linee oblique rispetto al piano di proiezione appaiono accorciate. Solo le linee parallele al piano di proiezione mantengono la loro lunghezza reale.
- Scelta del Piano di Proiezione: La scelta del piano di proiezione influenza significativamente l'aspetto della proiezione. È importante scegliere un piano che mostri le caratteristiche principali dell'oggetto.
Per superare queste limitazioni, spesso si utilizzano più proiezioni ortogonali (ad esempio, pianta, prospetto, sezione) per fornire una rappresentazione completa dell'oggetto. Inoltre, si possono utilizzare proiezioni prospettiche per creare immagini più realistiche che tengano conto della profondità.
Conclusioni
La proiezione ortogonale è un concetto essenziale per la rappresentazione e la comprensione di oggetti tridimensionali. La sua applicazione spazia dall'architettura all'ingegneria, dal design alla grafica computerizzata. Comprendere i principi fondamentali della proiezione ortogonale, inclusi i suoi vantaggi e le sue limitazioni, è cruciale per chiunque lavori con la geometria spaziale. Invitiamo il lettore ad approfondire ulteriormente l'argomento, sperimentando con diversi strumenti di disegno e software CAD per acquisire una padronanza pratica di questa tecnica fondamentale. La capacità di visualizzare e manipolare mentalmente le proiezioni ortogonali è un'abilità preziosa in molti campi.
Esercizio: Prendi un oggetto semplice, come una scatola, e prova a disegnarne le proiezioni ortogonali su tre piani perpendicolari tra loro (pianta, prospetto, sezione). Questo esercizio ti aiuterà a visualizzare come l'oggetto appare da diverse angolazioni e a comprendere meglio il concetto di proiezione ortogonale.