Ciao! Immagina di dover spiegare a un amico come arrivare a un punto preciso sulla mappa, usando solo numeri. Oppure, pensa di dover calcolare la distanza tra due oggetti sullo schermo del tuo computer. Ecco, in entrambi i casi, la lunghezza di un segmento sul piano cartesiano diventa uno strumento potentissimo. Magari sembra una cosa astratta studiata a scuola, ma in realtà ci circonda e ci aiuta a risolvere problemi concreti ogni giorno.
Perché Dovresti Preoccuparti della Lunghezza di un Segmento?
Forse ti stai chiedendo: "Ma a me cosa importa?". La risposta è semplice: questa conoscenza ha applicazioni sorprendenti. Non si tratta solo di fare esercizi di matematica. Pensa a:
- Navigazione GPS: Il tuo navigatore calcola continuamente distanze tra punti sulla mappa per darti il percorso più breve.
- Grafica Computerizzata: Per disegnare linee, poligoni e oggetti 3D, i computer devono calcolare lunghezze e distanze tra punti.
- Architettura e Ingegneria: Per progettare edifici e infrastrutture, è fondamentale calcolare distanze e dimensioni con precisione.
- Videogiochi: Il movimento dei personaggi, la distanza degli oggetti, tutto dipende da calcoli geometrici che includono la lunghezza dei segmenti.
In sintesi, la lunghezza di un segmento sul piano cartesiano è un concetto fondamentale in moltissime discipline. Capire come calcolarla ti apre le porte a un mondo di possibilità.
Il Piano Cartesiano: Un Breve Ripasso
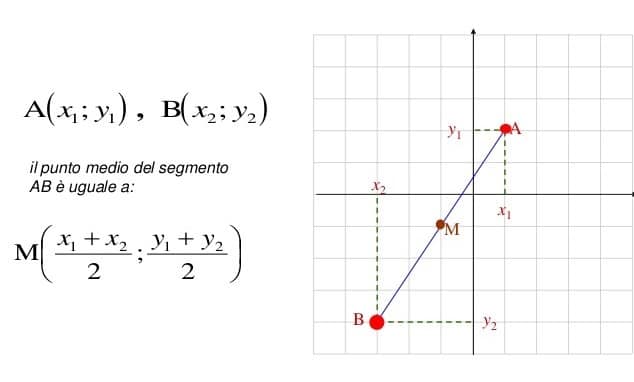
Prima di addentrarci nel calcolo della lunghezza, rinfreschiamo le basi. Il piano cartesiano è un sistema di coordinate bidimensionale formato da due rette perpendicolari: l'asse delle ascisse (asse x) e l'asse delle ordinate (asse y). Queste due rette si intersecano in un punto chiamato origine, che corrisponde al punto (0, 0).
Ogni punto sul piano cartesiano è identificato da una coppia ordinata di numeri (x, y), dove x rappresenta la sua posizione sull'asse delle ascisse e y rappresenta la sua posizione sull'asse delle ordinate.
Ad esempio, il punto (3, 2) si trova a 3 unità a destra dell'origine sull'asse x e a 2 unità sopra l'origine sull'asse y.
La Formula Magica: Come Calcolare la Lunghezza di un Segmento
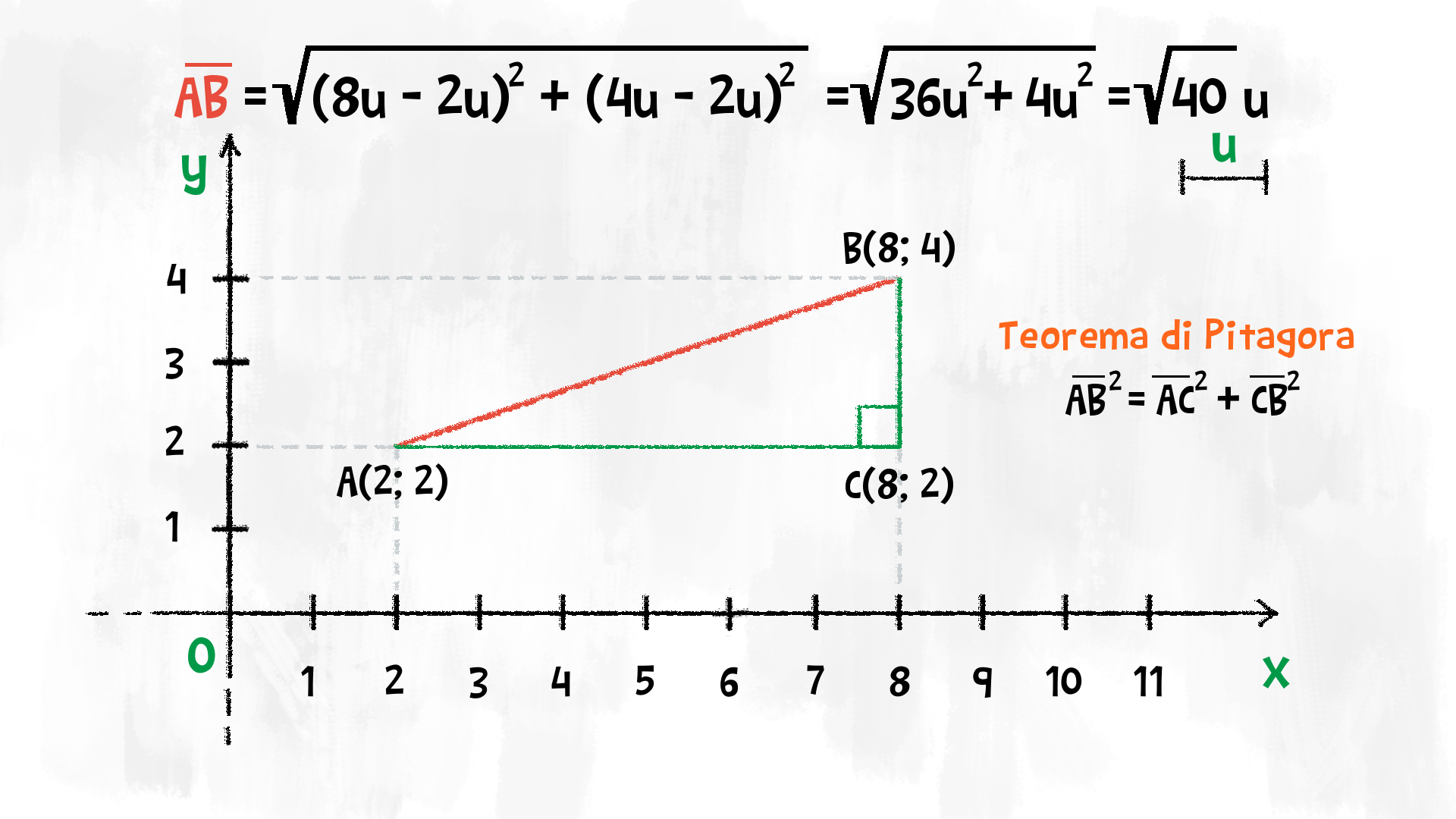
Ora veniamo al dunque. Supponiamo di avere due punti sul piano cartesiano: A(x1, y1) e B(x2, y2). La lunghezza del segmento AB, che indicheremo con |AB|, si calcola con la seguente formula:
|AB| = √((x2 - x1)2 + (y2 - y1)2)
Questa formula sembra complicata, ma in realtà è basata su un teorema che probabilmente conosci già: il teorema di Pitagora!

Il Teorema di Pitagora e la Lunghezza del Segmento
Immagina di disegnare un triangolo rettangolo con i seguenti vertici: A(x1, y1), B(x2, y2) e C(x2, y1). Il segmento AB è l'ipotenusa di questo triangolo, mentre i segmenti AC e BC sono i cateti.
La lunghezza del cateto AC è data da |x2 - x1|, mentre la lunghezza del cateto BC è data da |y2 - y1|.
Secondo il teorema di Pitagora, il quadrato dell'ipotenusa (AB) è uguale alla somma dei quadrati dei cateti (AC e BC):
|AB|2 = |AC|2 + |BC|2
|AB|2 = (x2 - x1)2 + (y2 - y1)2
Per trovare la lunghezza di AB, dobbiamo semplicemente calcolare la radice quadrata di entrambi i membri dell'equazione:
|AB| = √((x2 - x1)2 + (y2 - y1)2)
Ed ecco la formula che abbiamo visto prima! Come vedi, non è magia, ma solo una brillante applicazione di un teorema fondamentale.
Esempio Pratico: Calcoliamo la Lunghezza di un Segmento
Per rendere tutto più chiaro, facciamo un esempio concreto. Supponiamo di avere i punti A(1, 2) e B(4, 6). Vogliamo calcolare la lunghezza del segmento AB.
Applichiamo la formula:
|AB| = √((4 - 1)2 + (6 - 2)2)
|AB| = √((3)2 + (4)2)

|AB| = √(9 + 16)
|AB| = √25
|AB| = 5
Quindi, la lunghezza del segmento AB è di 5 unità.
Possibili Obiezioni e Controargomentazioni
Qualcuno potrebbe dire: "Ma questa formula è inutile! Posso semplicemente misurare la distanza con un righello!". Certo, in alcuni casi puoi farlo, ma immagina di dover calcolare la distanza tra due stelle nel cielo, o tra due punti su una mappa digitale. In questi casi, la formula diventa indispensabile.
Un altro potrebbe obiettare: "Questa è solo teoria, non serve a niente nella vita reale!". Come abbiamo visto all'inizio, la lunghezza di un segmento è fondamentale in moltissime applicazioni pratiche, dalla navigazione GPS alla grafica computerizzata. Anche se non te ne rendi conto, la usi (o la userai) più spesso di quanto pensi.
Consigli Utili per Evitare Errori
Ecco alcuni consigli per evitare errori quando calcoli la lunghezza di un segmento:
- Fai attenzione ai segni: Ricorda che (x2 - x1) può essere positivo o negativo. Assicurati di elevare al quadrato il risultato corretto.
- Usa le parentesi: Utilizza le parentesi per raggruppare i termini correttamente e evitare errori di calcolo.
- Verifica il risultato: Dopo aver calcolato la lunghezza, controlla se il risultato è ragionevole. Ad esempio, la lunghezza di un segmento non può essere negativa.
- Disegna un grafico: Se hai difficoltà a visualizzare il problema, disegna un grafico dei punti sul piano cartesiano. Questo può aiutarti a capire meglio la situazione.
Oltre la Formula: Comprendere il Concetto
Ricorda che la formula è solo uno strumento. L'importante è capire il concetto che c'è dietro: la lunghezza di un segmento è l'ipotenusa di un triangolo rettangolo, e possiamo calcolarla usando il teorema di Pitagora. Se comprendi questo, la formula diventerà molto più facile da ricordare e da applicare.
Il Potere della Visualizzazione
Spesso, la difficoltà nel comprendere concetti matematici risiede nell'astrazione. Per rendere tutto più concreto, prova a visualizzare mentalmente il segmento come un lato di un triangolo rettangolo. Immagina i cateti che si proiettano sugli assi x e y. Questo approccio può aiutarti a interiorizzare la formula e a capire perché funziona.
Prossimi Passi: Metti in Pratica le Tue Nuove Conoscenze
Ora che hai imparato a calcolare la lunghezza di un segmento sul piano cartesiano, è il momento di mettere in pratica le tue nuove conoscenze. Prova a risolvere alcuni esercizi. Cerca online esercizi di geometria analitica. Oppure, inventa i tuoi punti e calcola la distanza tra di essi.
La pratica è fondamentale per consolidare ciò che hai imparato. Più esercizi farai, più diventerai bravo e sicuro di te.
Ricorda, la matematica non è solo una serie di formule da memorizzare, ma un modo di pensare e di risolvere problemi. Continua a esplorare, a sperimentare e a mettere in discussione ciò che impari. La matematica è un'avventura che dura tutta la vita!
Ti sei mai chiesto come la lunghezza di un segmento potrebbe essere utilizzata nel tuo campo di interesse? Riflettici su e magari scoprirai nuove, inaspettate applicazioni!