Ti sei mai trovato a fissare un barattolo di fagioli o la punta di un cono gelato, chiedendoti che cosa li accomuni oltre alla loro forma apparentemente diversa? Magari hai sempre pensato che cilindri e coni fossero mondi a sé stanti in geometria, entità separate con regole proprie. Beh, preparati a una piccola rivelazione: in geometria, il cilindro è sia il cilindro che, in un certo senso, una forma conica. Sembra un paradosso? Cerchiamo di svelare questo legame affascinante, passo dopo passo.
Cilindri e Coni: Un'Introduzione
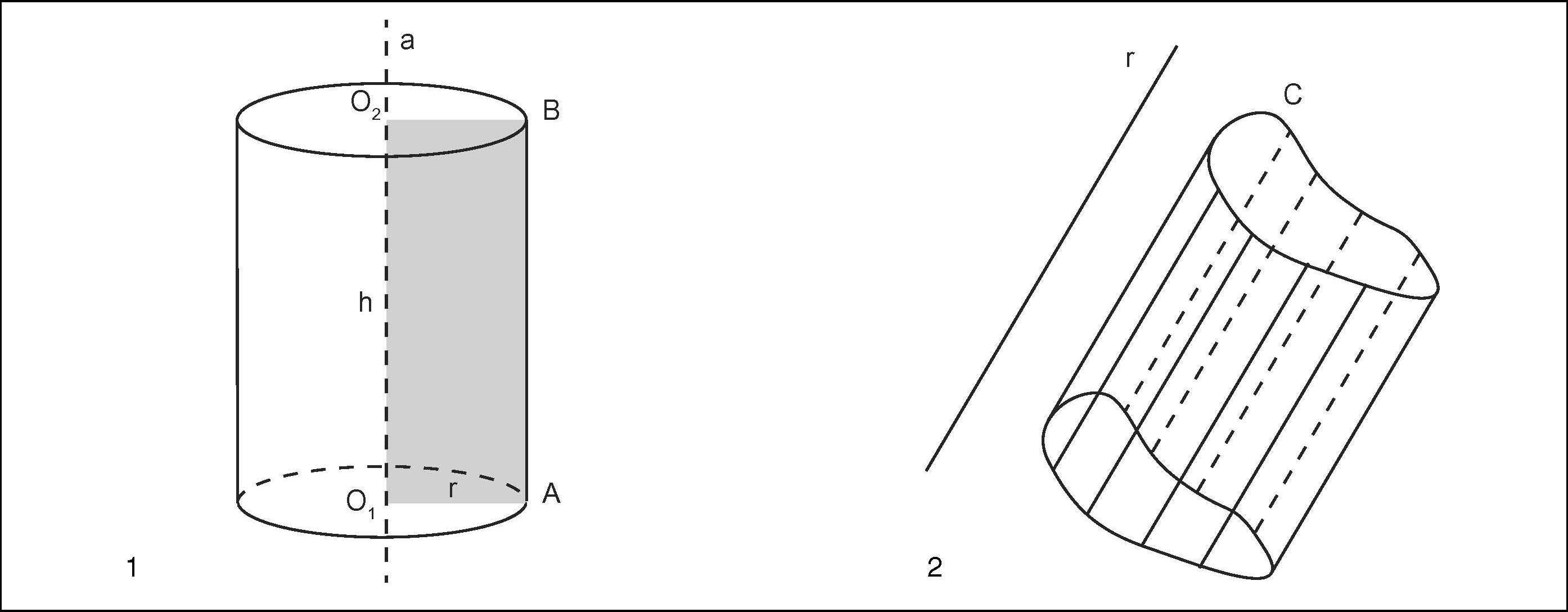
Partiamo dalle basi. Cos'è un cilindro? Generalmente, lo definiamo come un solido geometrico con due basi congruenti e parallele (solitamente cerchi) connesse da una superficie laterale curva. Pensiamo a un tubo, a una lattina, o anche a un tronco d'albero. La sua caratteristica principale è che mantiene la stessa sezione trasversale lungo tutta la sua altezza.
E il cono? Immagina un cappello da festa, la punta di una matita o un megafono. Un cono è un solido geometrico che ha una base (di solito un cerchio) e un vertice (o apice) che non si trova sullo stesso piano della base. La superficie laterale del cono si restringe gradualmente man mano che si avvicina al vertice.
La Chiave Sta nella Definizione
La parola chiave qui è la definizione matematica rigorosa. In matematica, soprattutto a livello avanzato, si parla spesso di "coni generalizzati". Un cono generalizzato non deve necessariamente avere una base circolare o restringersi fino a un punto. La definizione più ampia è questa: un cono è la figura geometrica formata da tutte le rette passanti per un punto fisso (il vertice) e per ogni punto di una curva chiusa (la base).
Capito? Se la curva chiusa (la base) è un cerchio e il vertice si trova esattamente sopra il centro del cerchio, perpendicolarmente, allora abbiamo il cono "classico" che conosciamo. Ma... cosa succede se il vertice è infinitamente lontano?
Il Cilindro Come Cono Generalizzato
Qui arriviamo al punto cruciale. Se il vertice del nostro cono ipotetico si allontana all'infinito, le rette che lo collegano alla base diventano sempre più parallele. In questo scenario, la superficie conica non si restringe più, ma diventa una superficie cilindrica. In altre parole, un cilindro può essere considerato un cono generalizzato con un vertice all'infinito. Questo è un concetto importante nell'ambito della geometria proiettiva.
Per visualizzarlo, immagina di allungare sempre di più un cono. Man mano che lo allunghi, la sua punta diventa sempre più lontana e le sue pareti tendono a diventare sempre più parallele. All'infinito, questo "cono allungato" si trasforma in un cilindro.
Implicazioni Pratiche e Teoriche
Forse ti stai chiedendo: "A cosa serve tutto questo? Mica devo progettare grattacieli che cambiano forma!". Ed è vero, nella vita di tutti i giorni non ci troviamo a pensare a coni infinitamente allungati. Però, questa comprensione ha delle implicazioni importanti in diversi campi:

Grafica Computerizzata
Nella grafica computerizzata, questa equivalenza semplifica notevolmente gli algoritmi. Trattare cilindri e coni come casi speciali della stessa entità geometrica permette di scrivere codice più efficiente e versatile. Pensiamo alla modellazione 3D, dove si costruiscono oggetti complessi a partire da forme geometriche fondamentali.
Progettazione Architettonica e Ingegneria
Architetti e ingegneri utilizzano spesso software CAD (Computer-Aided Design) che sfruttano queste proprietà matematiche per la modellazione e l'analisi strutturale. Capire la relazione tra cilindri e coni permette di ottimizzare il design e prevedere il comportamento delle strutture.
Geometria Proiettiva
Come accennato, la geometria proiettiva è il campo che studia le proprietà geometriche che rimangono invariate sotto proiezioni. In questa geometria, concetti come parallelismo e distanza perdono la loro importanza. Un cilindro e un cono diventano quindi proiettivamente equivalenti, cioè possono essere trasformati l'uno nell'altro attraverso una proiezione. Questo è un concetto fondamentale per comprendere le trasformazioni geometriche e le loro applicazioni.

Un Esempio Concreto
Immagina di proiettare l'ombra di un cilindro su una superficie piana. A seconda dell'angolo di proiezione, l'ombra può apparire come un cilindro (se la luce è parallela all'asse del cilindro), o come una forma più simile a un cono (se la luce è inclinata). Questo dimostra visivamente come la stessa figura (il cilindro) possa apparire diversa a seconda della prospettiva, e come la geometria proiettiva ci aiuti a comprendere queste trasformazioni.
Oltre la Forma: Proprietà Comuni
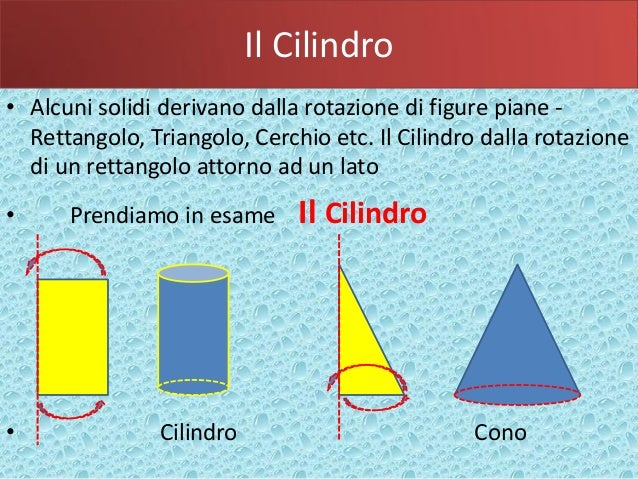
Oltre alla definizione matematica, cilindri e coni condividono anche alcune proprietà fondamentali: entrambi sono solidi di rotazione, il che significa che possono essere generati facendo ruotare una figura piana attorno a un asse. Nel caso del cilindro, la figura piana è un rettangolo; nel caso del cono, è un triangolo rettangolo. Questa proprietà condivisa sottolinea ulteriormente il loro legame.
Inoltre, sia il cilindro che il cono hanno una superficie laterale sviluppabile, cioè possono essere "appiattiti" su un piano senza distorsioni. Questo è particolarmente evidente nel caso del cono, che può essere tagliato lungo un lato e dispiegato in un settore circolare. Anche il cilindro può essere tagliato lungo la sua altezza e dispiegato in un rettangolo.

Conclusione: Una Prospettiva Più Ampia
La prossima volta che vedrai un cilindro o un cono, spero che ti ricorderai di questa connessione inaspettata. Comprendere che il cilindro può essere considerato un caso limite del cono non è solo un esercizio teorico, ma ci fornisce una prospettiva più ampia e profonda sulla geometria e sulle sue applicazioni nel mondo reale.
Non si tratta solo di imparare formule a memoria, ma di sviluppare un pensiero critico e la capacità di vedere le cose da diverse angolazioni. E forse, la prossima volta che ti godrai un cono gelato, lo farai con una maggiore consapevolezza della sua complessa e affascinante relazione con il suo apparentemente più semplice cugino cilindrico.
Quindi, la risposta alla domanda iniziale è sì: in un certo senso, in geometria, il cilindro lo è sia il cilindro che una forma conica. Un po' come dire che un quadrato è anche un rettangolo, ma con una marcia in più di astrazione e bellezza matematica!