Avete mai pensato a come descrivere una linea retta che taglia esattamente il cuore del sistema di coordinate? Parliamo oggi di un concetto fondamentale in matematica: l'equazione di una retta passante per l'origine. Questo articolo è pensato per studenti delle scuole superiori e università, ma anche per chiunque voglia rinfrescare o approfondire le proprie conoscenze di geometria analitica. Cercheremo di rendere il tutto il più chiaro e intuitivo possibile, partendo dai concetti base e arrivando a esempi concreti.
Cosa significa "passare per l'origine"?
Prima di addentrarci nell'equazione, chiariamo cosa intendiamo quando diciamo che una retta "passa per l'origine". L'origine è il punto in cui gli assi cartesiani x e y si incontrano. Le sue coordinate sono (0, 0). Quindi, una retta passante per l'origine è semplicemente una linea retta che interseca il piano cartesiano proprio in quel punto.
L'equazione: y = mx
L'equazione che descrive una retta passante per l'origine è incredibilmente semplice:
y = mx
Dove:
- y rappresenta la coordinata verticale (ordinata) di un punto qualsiasi sulla retta.
- x rappresenta la coordinata orizzontale (ascissa) di un punto qualsiasi sulla retta.
- m è il coefficiente angolare o pendenza della retta.
Il coefficiente angolare (m) è la chiave per capire l'inclinazione della retta rispetto all'asse x. Ci dice di quanto varia y quando x aumenta di una unità. Un valore positivo di m indica che la retta sale (va verso l'alto) da sinistra a destra, mentre un valore negativo indica che la retta scende (va verso il basso) da sinistra a destra. Se m è zero, la retta è orizzontale e coincide con l'asse x (y = 0).
Comprendere il Coefficiente Angolare (m)
Il coefficiente angolare m si calcola come il rapporto tra la variazione di y (Δy) e la variazione di x (Δx) tra due punti qualsiasi sulla retta:
m = Δy / Δx
Poiché la retta passa per l'origine (0,0), possiamo scegliere un altro punto qualsiasi sulla retta, ad esempio (x, y), e calcolare m come:

m = (y - 0) / (x - 0) = y / x
Questo conferma che y = mx è l'equazione corretta per una retta passante per l'origine.
Esempi Pratici
Vediamo alcuni esempi per rendere il concetto ancora più chiaro:
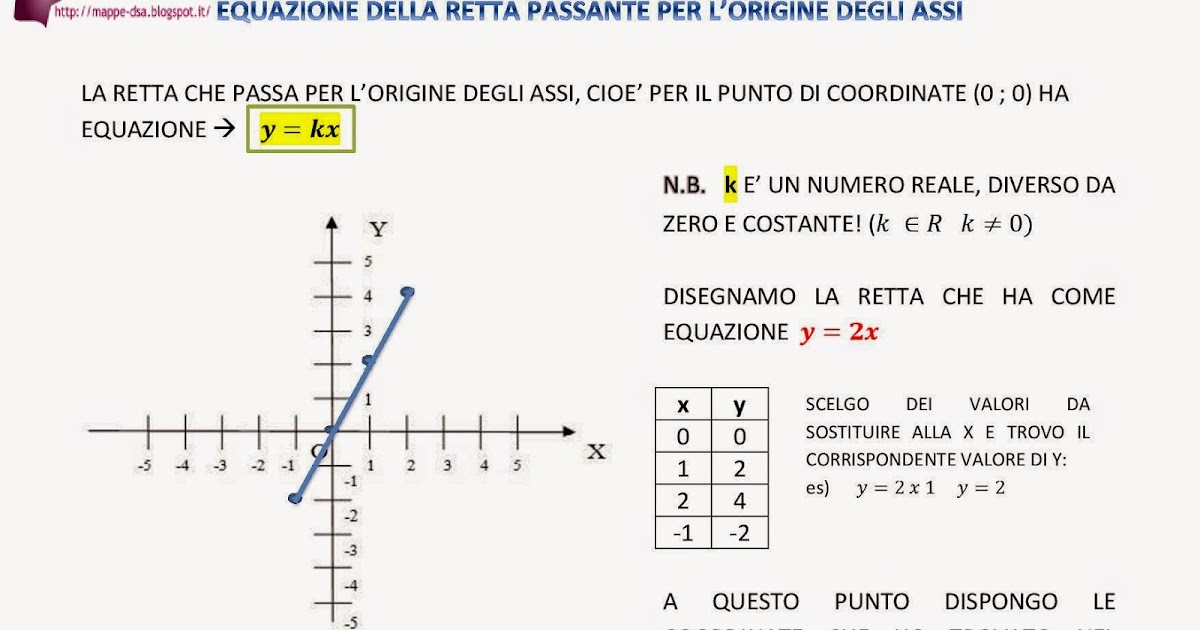
- Esempio 1: y = 2x
In questo caso, il coefficiente angolare è m = 2. Significa che per ogni unità che ci spostiamo verso destra sull'asse x, ci spostiamo di 2 unità verso l'alto sull'asse y. La retta è abbastanza ripida e sale verso l'alto.

EQUAZIONE DI UNA RETTA PER L'ORIGINE - lezioniignoranti - Esempio 2: y = -x
Qui, m = -1. Per ogni unità che ci spostiamo verso destra sull'asse x, ci spostiamo di 1 unità verso il basso sull'asse y. La retta scende verso il basso.
- Esempio 3: y = (1/3)x
In questo caso, m = 1/3. Per ogni 3 unità che ci spostiamo verso destra sull'asse x, ci spostiamo di 1 unità verso l'alto sull'asse y. La retta è meno ripida rispetto all'esempio 1.
Possiamo verificare che questi esempi passano per l'origine sostituendo x = 0 nell'equazione. In ogni caso, otteniamo y = 0, confermando che il punto (0, 0) appartiene alla retta.
Come disegnare una retta passante per l'origine
Disegnare una retta di questo tipo è molto semplice. Abbiamo bisogno di un solo punto, oltre all'origine.

- Identifica il coefficiente angolare (m) nell'equazione y = mx.
- Scegli un valore qualsiasi per x (diverso da zero).
- Calcola il valore corrispondente di y utilizzando l'equazione y = mx.
- Ora hai due punti: l'origine (0, 0) e il punto (x, y) che hai calcolato.
- Traccia una linea retta che passa attraverso questi due punti.
Ad esempio, per la retta y = 3x, potremmo scegliere x = 1. Allora y = 3 * 1 = 3. Abbiamo quindi i punti (0, 0) e (1, 3). Uniamo questi due punti con una retta e abbiamo il grafico della retta y = 3x.
Applicazioni Pratiche
Le rette passanti per l'origine non sono solo un concetto teorico. Trovano applicazione in molte aree, tra cui:
- Fisica: Descrivere la relazione tra velocità e tempo nel moto uniforme (v = at, dove a è l'accelerazione).
- Economia: Rappresentare relazioni lineari tra domanda e offerta in modelli semplificati.
- Informatica: Calcolare proporzioni e scaling in grafica computerizzata.
- Geometria: Determinare se un punto appartiene a una retta specifica che passa per l'origine.
Ad esempio, in fisica, se un oggetto si muove a velocità costante, la distanza percorsa è direttamente proporzionale al tempo trascorso. Questa relazione può essere rappresentata da una retta passante per l'origine, dove la velocità è il coefficiente angolare.
Differenza con l'equazione generale di una retta
È importante distinguere l'equazione y = mx dall'equazione generale di una retta, che è y = mx + q. La differenza fondamentale è la presenza del termine q, chiamato intercetta. L'intercetta indica il punto in cui la retta interseca l'asse y. Se q = 0, la retta passa per l'origine e l'equazione si riduce a y = mx.
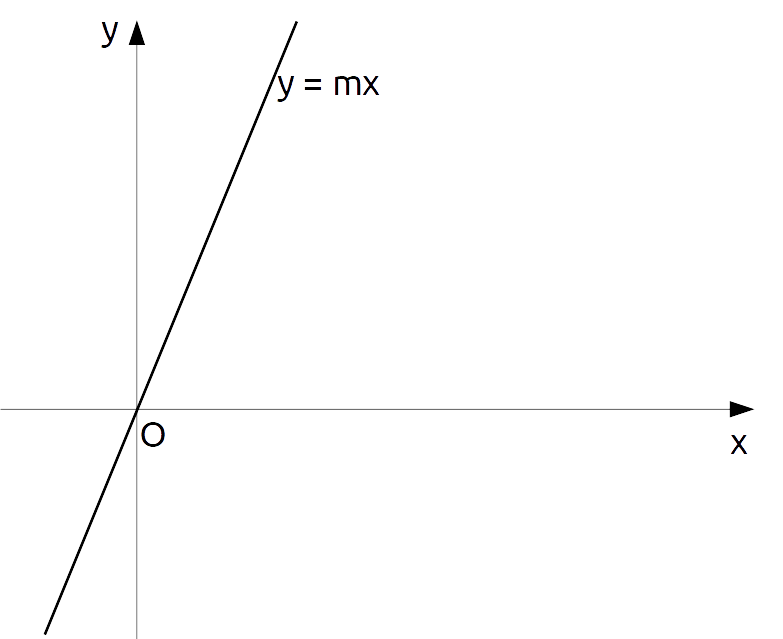
Quindi, l'equazione y = mx è un caso speciale dell'equazione generale di una retta, in cui l'intercetta è zero.
Esercizi per Mettere alla Prova le Tue Conoscenze
Per consolidare ciò che hai imparato, prova a risolvere questi semplici esercizi:
- Trova l'equazione della retta passante per l'origine e per il punto (2, 6).
- Disegna le rette y = -2x e y = (1/2)x sullo stesso piano cartesiano.
- Un oggetto si muove a velocità costante di 5 m/s. Scrivi l'equazione che descrive la relazione tra distanza percorsa (y) e tempo (x).
Questi esercizi ti aiuteranno a familiarizzare con il concetto e a applicarlo in diverse situazioni.
Conclusione
L'equazione di una retta passante per l'origine (y = mx) è uno strumento potente e versatile in matematica e in molte altre discipline. La sua semplicità non deve ingannare: con un solo parametro, il coefficiente angolare, possiamo descrivere l'inclinazione e la direzione di una retta che taglia il cuore del sistema di coordinate. Speriamo che questo articolo ti abbia aiutato a comprendere meglio questo concetto fondamentale e a vedere le sue applicazioni nel mondo reale. Ricorda, la matematica è come un linguaggio: più la pratichi, più fluente diventi! Continua a esplorare, a sperimentare e a porre domande. Il mondo della matematica è vasto e affascinante, e c'è sempre qualcosa di nuovo da scoprire.