
Quante volte, studiando fisica, ci siamo sentiti sopraffatti dalla complessità dell'atomo? Cerchiamo di immaginarci minuscoli, quasi al livello subatomico, e proviamo a seguire un elettrone mentre sfreccia intorno al nucleo. Comprendere la sua energia cinetica può sembrare un'impresa ardua, ma in realtà è una chiave fondamentale per sbloccare molti segreti della materia.
Un Viaggio Nell'Atomo: Preparazione al Concetto di Energia Cinetica
Prima di immergerci nei calcoli e nelle formule, è importante avere ben chiari alcuni concetti di base. Immagina l'atomo come un piccolo sistema solare: al centro troviamo il nucleo, composto da protoni e neutroni, e intorno orbitano gli elettroni. Questi elettroni non sono statici, ma sono in costante movimento. È proprio questo movimento che genera l'energia cinetica.
Cos'è l'Energia Cinetica?
L'energia cinetica, in termini semplici, è l'energia che un oggetto possiede a causa del suo movimento. Più un oggetto è veloce e più è massivo, maggiore sarà la sua energia cinetica. La formula base per calcolare l'energia cinetica (Ec) è: Ec = 1/2 * m * v2, dove 'm' è la massa dell'oggetto e 'v' è la sua velocità. Quindi, per un elettrone in orbita, l'energia cinetica dipende dalla sua massa e dalla sua velocità orbitale.
Energia Cinetica di un Elettrone in Orbita: Un'Analisi Approfondita
Ora affrontiamo il cuore del problema: come calcoliamo l'energia cinetica di un elettrone in orbita? La risposta non è così semplice come applicare direttamente la formula Ec = 1/2 * m * v2. Dobbiamo considerare alcuni aspetti specifici del modello atomico.
Il Modello Atomico di Bohr e la Quantizzazione dell'Energia
Un punto di partenza cruciale è il modello atomico di Bohr. Niels Bohr, nel 1913, propose che gli elettroni potessero orbitare intorno al nucleo solo su determinate orbite, chiamate orbite stazionarie, con livelli di energia ben definiti. Questo significa che l'energia dell'elettrone non può assumere qualsiasi valore, ma è quantizzata. Come afferma David Griffiths nel suo libro "Introduction to Quantum Mechanics," la quantizzazione è un concetto fondamentale per comprendere il comportamento degli atomi. (Griffiths, D.J. (2004). Introduction to Quantum Mechanics. Pearson Education.)

Calcolare la Velocità dell'Elettrone: Un Passo Fondamentale
Per calcolare l'energia cinetica, abbiamo bisogno della velocità (v) dell'elettrone. Nel modello di Bohr, la velocità di un elettrone in un'orbita specifica è legata al numero quantico principale 'n' (n = 1, 2, 3...). La formula per la velocità (v) in un'orbita di Bohr è approssimativamente: v = (e2) / (2 * ε0 * h * n), dove: * 'e' è la carica elementare dell'elettrone (circa 1.602 x 10-19 Coulomb). * 'ε0' è la permittività del vuoto (circa 8.854 x 10-12 F/m). * 'h' è la costante di Planck (circa 6.626 x 10-34 J s). * 'n' è il numero quantico principale (1, 2, 3...).
È importante notare che questa è una semplificazione e che la velocità reale può variare a seconda dell'atomo e dell'orbita specifica. Tuttavia, fornisce una buona approssimazione per comprendere il concetto.

L'Energia Totale e l'Energia Cinetica
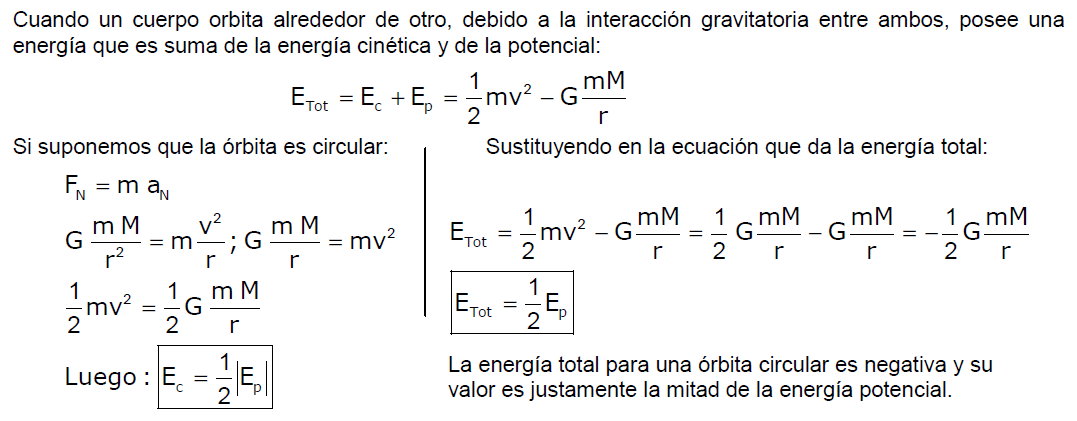
Un altro aspetto importante da considerare è l'energia totale dell'elettrone. L'energia totale (E) di un elettrone in un'orbita di Bohr è la somma della sua energia cinetica (Ec) e della sua energia potenziale (Ep). E = Ec + Ep. L'energia potenziale è dovuta all'attrazione elettrostatica tra l'elettrone e il nucleo carico positivamente. Nel modello di Bohr, si dimostra che l'energia cinetica è uguale al valore assoluto della metà dell'energia totale: Ec = |E/2|.
L'energia totale dell'elettrone in un'orbita di Bohr è data da: E = - (me * e4) / (8 * ε02 * h2 * n2), dove 'me' è la massa dell'elettrone (circa 9.109 x 10-31 kg). Quindi, l'energia cinetica sarà: Ec = (me * e4) / (16 * ε02 * h2 * n2).
Implicazioni della Quantizzazione dell'Energia Cinetica
La quantizzazione dell'energia implica che l'elettrone può avere solo determinati valori di energia cinetica, corrispondenti alle diverse orbite permesse. Ad esempio, l'elettrone nell'orbita più vicina al nucleo (n = 1) avrà l'energia cinetica più alta, mentre l'elettrone in un'orbita più lontana (n = 2, 3, etc.) avrà un'energia cinetica inferiore. Questo concetto è fondamentale per comprendere gli spettri di emissione e assorbimento degli atomi, che sono alla base di molte tecnologie, come i laser e le lampade fluorescenti.
Come Applicare Questi Concetti: Esercizi e Strumenti Pratici
Ora che abbiamo visto la teoria, mettiamo in pratica quello che abbiamo imparato. Ecco alcuni esempi e suggerimenti per applicare questi concetti:

- Calcolo dell'Energia Cinetica per Diverse Orbite: Prendi un atomo semplice, come l'idrogeno, e calcola l'energia cinetica dell'elettrone per le prime tre orbite (n = 1, 2, 3) usando le formule che abbiamo visto. Questo ti darà un'idea di come l'energia cinetica diminuisce all'aumentare della distanza dal nucleo.
- Simulazioni Interattive: Esistono molte simulazioni online che permettono di visualizzare il modello atomico di Bohr e di manipolare i livelli di energia degli elettroni. Queste simulazioni possono essere molto utili per comprendere visivamente come l'energia cinetica è legata all'orbita dell'elettrone. Phet Colorado offre delle simulazioni interattive eccellenti (cerca "Bohr Model Phet").
- Risoluzione di Problemi: Cerca esercizi di fisica che coinvolgono il calcolo dell'energia cinetica di un elettrone in un atomo. Questo ti aiuterà a consolidare la tua comprensione dei concetti e delle formule.
- Analisi di Spettri Atomici: Studia gli spettri di emissione di diversi elementi. Le righe spettrali corrispondono alle transizioni degli elettroni tra i diversi livelli di energia. Comprendere l'energia cinetica degli elettroni ti aiuterà a interpretare questi spettri.
Oltre il Modello di Bohr: Un'Introduzione alla Meccanica Quantistica
È importante sottolineare che il modello di Bohr è una semplificazione. La vera descrizione del comportamento degli elettroni negli atomi è fornita dalla meccanica quantistica. In meccanica quantistica, gli elettroni non orbitano intorno al nucleo su orbite fisse, ma sono descritti da funzioni d'onda, che rappresentano la probabilità di trovare l'elettrone in una determinata regione dello spazio. Anche l'energia cinetica, in questo contesto, è un operatore quantistico, e il suo valore medio può essere calcolato usando la funzione d'onda.
Anche se la meccanica quantistica può sembrare complessa, i concetti che abbiamo visto, come la quantizzazione dell'energia e l'importanza della velocità dell'elettrone, rimangono validi. Il modello di Bohr è un utile punto di partenza per comprendere la fisica atomica, e fornisce una solida base per affrontare concetti più avanzati.
Conclusione: Un'Energia Nascosta che Definisce la Materia
Comprendere l'energia cinetica di un elettrone in orbita non è solo un esercizio teorico. È una chiave per sbloccare la comprensione di come funziona la materia a livello fondamentale. Dalla stabilità degli atomi alle proprietà chimiche degli elementi, l'energia cinetica degli elettroni gioca un ruolo cruciale. Quindi, la prossima volta che ti troverai a studiare fisica, ricorda che anche le particelle più piccole, come gli elettroni, sono in costante movimento, e che la loro energia cinetica è una forza potente che plasma il mondo che ci circonda. Come diceva Richard Feynman, "Se pensi di aver capito la meccanica quantistica, allora non hai capito la meccanica quantistica." (Feynman, R. P. (1985). QED: The Strange Theory of Light and Matter. Princeton University Press.) Continuiamo quindi ad esplorare e interrogarci, perché la bellezza della scienza risiede proprio nella sua capacità di sorprenderci e di aprirci nuove prospettive.