Ciao a tutti! So che a volte la matematica può sembrare una montagna difficile da scalare, con concetti che sembrano ostacoli insormontabili. Oggi vorrei parlare di un argomento che può apparire spaventoso all'inizio: le discontinuità. Ma fidatevi, capire le discontinuità di prima, seconda e terza specie è come imparare una nuova lingua. All'inizio sembra complicato, ma una volta compresi i meccanismi di base, si aprono nuove prospettive.
Perché preoccuparsi delle discontinuità?
Potreste chiedervi: "Perché dovrei studiare le discontinuità? A cosa mi serve nella vita reale?". La risposta è semplice: le discontinuità sono ovunque! Immaginate un grafico che rappresenta la temperatura in una stanza. Se all'improvviso si rompe il termostato e la temperatura fa un salto improvviso, ecco una discontinuità. Oppure, pensate al livello dell'acqua in un serbatoio che viene riempito a intermittenza. Le discontinuità ci aiutano a modellare e a comprendere fenomeni che non sono sempre fluidi e continui.
La bellezza della sfida
Capire le discontinuità non è solo utile, ma anche gratificante. Affrontare una sfida matematica e superarla ci rende più forti e sicuri di noi stessi. Ogni volta che risolvete un esercizio sulle discontinuità, state affinando le vostre capacità di problem solving e di pensiero critico. State imparando a guardare i problemi da diverse angolazioni, a scomporli in parti più piccole e a trovare soluzioni creative.
Discontinuità di prima specie: un salto nel vuoto (o quasi)
La discontinuità di prima specie è come un piccolo salto. La funzione si avvicina a un valore da sinistra e a un altro valore da destra. Pensate a una rampa: vi avvicinate da un lato, poi fate un salto e continuate dall'altro. È importante notare che il limite destro e il limite sinistro esistono, ma sono diversi tra loro. Superare questa difficoltà significa allenare la mente a considerare diversi approcci alla soluzione. Vi preparate ad affrontare situazioni complesse nel vostro futuro.
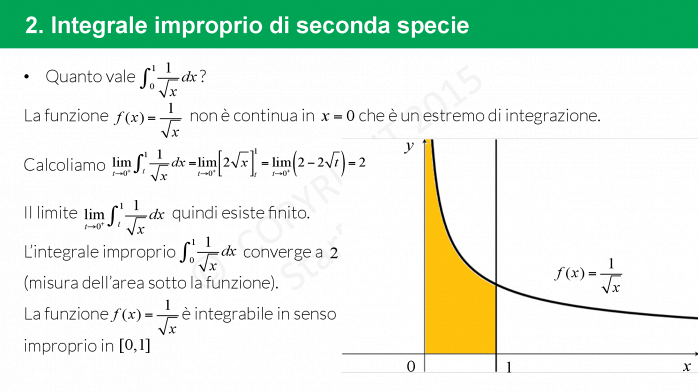
Discontinuità di seconda specie: l'abisso infinito
La discontinuità di seconda specie è un po' più complicata. Qui, almeno uno dei due limiti (destro o sinistro) non esiste, oppure è infinito. È come trovarsi di fronte a un abisso: non si riesce a vedere la fine. Affrontare questo tipo di discontinuità vi insegna a non arrendervi di fronte all'apparente impossibilità di trovare una soluzione. Vi spinge a cercare alternative, a sperimentare e a non aver paura di sbagliare. È un esercizio di resilienza e di determinazione.
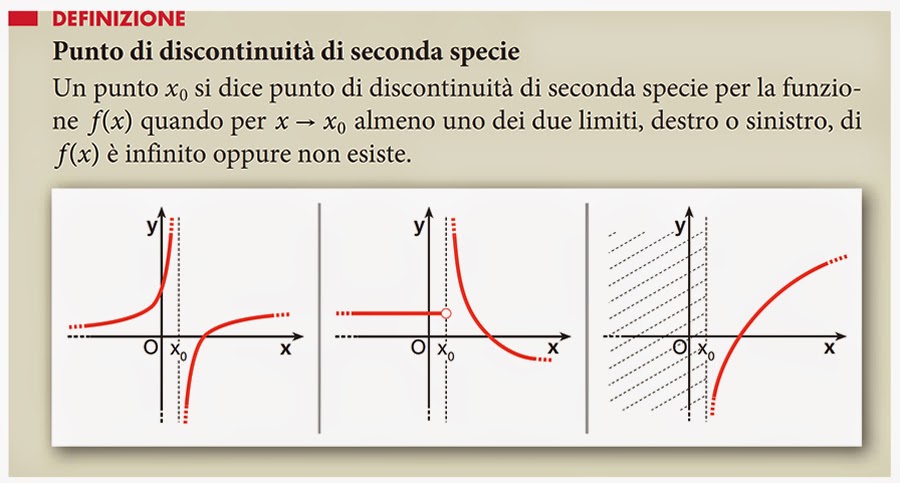
Discontinuità di terza specie (o eliminabile): l'inganno risolto
La discontinuità di terza specie, o eliminabile, è la più "gentile" delle tre. In questo caso, il limite della funzione esiste, ma la funzione non è definita in quel punto, oppure assume un valore diverso. È come un piccolo buco nel percorso, che può essere facilmente riempito. Riconoscere e "riempire" queste discontinuità vi aiuta a sviluppare un'attenzione al dettaglio e una precisione che saranno preziose in qualsiasi ambito della vostra vita.
Il successo è un percorso, non una destinazione
Ricordate, il percorso di apprendimento è fatto di alti e bassi. Ci saranno momenti in cui vi sentirete frustrati e scoraggiati, ma non arrendetevi! Chiedete aiuto ai vostri insegnanti, ai vostri compagni di classe, cercate risorse online. E soprattutto, siate pazienti con voi stessi. Ogni passo avanti, anche il più piccolo, è una vittoria.
Einstein diceva: "Non preoccuparti delle tue difficoltà in matematica. Posso assicurarti che le mie sono ancora maggiori". Questo ci ricorda che tutti, anche i più grandi geni, hanno affrontato delle sfide. L'importante è non aver paura di chiedere aiuto e di non smettere mai di imparare.
Le discontinuità, come molte altre cose nella vita, possono sembrare spaventose all'inizio, ma con impegno, perseveranza e un pizzico di curiosità, possono diventare un'opportunità per crescere e per raggiungere i vostri obiettivi. Credete in voi stessi e non smettete mai di sognare!