
Hai mai pensato a come descriviamo il mondo che ci circonda? Spesso usiamo numeri, ma non sempre un numero da solo è sufficiente. Immagina di dover spiegare a qualcuno dove hai parcheggiato l'auto. Dire semplicemente "a 20 metri" non è sufficiente, giusto? Devi specificare anche la direzione. Questo è il punto di partenza per capire la differenza tra grandezze scalari e grandezze vettoriali. Questo articolo è pensato per chiunque si avvicini per la prima volta alla fisica, studenti delle scuole superiori o semplicemente curiosi di capire meglio i concetti fondamentali.
Cosa sono le Grandezze?
Prima di addentrarci nelle differenze, chiariamo cosa intendiamo per "grandezza". In fisica, una grandezza è una proprietà di un fenomeno, corpo o sostanza che può essere misurata. Ad esempio, la lunghezza, la massa, il tempo, la temperatura sono tutte grandezze.
Grandezze Scalari: Solo il Valore Conta
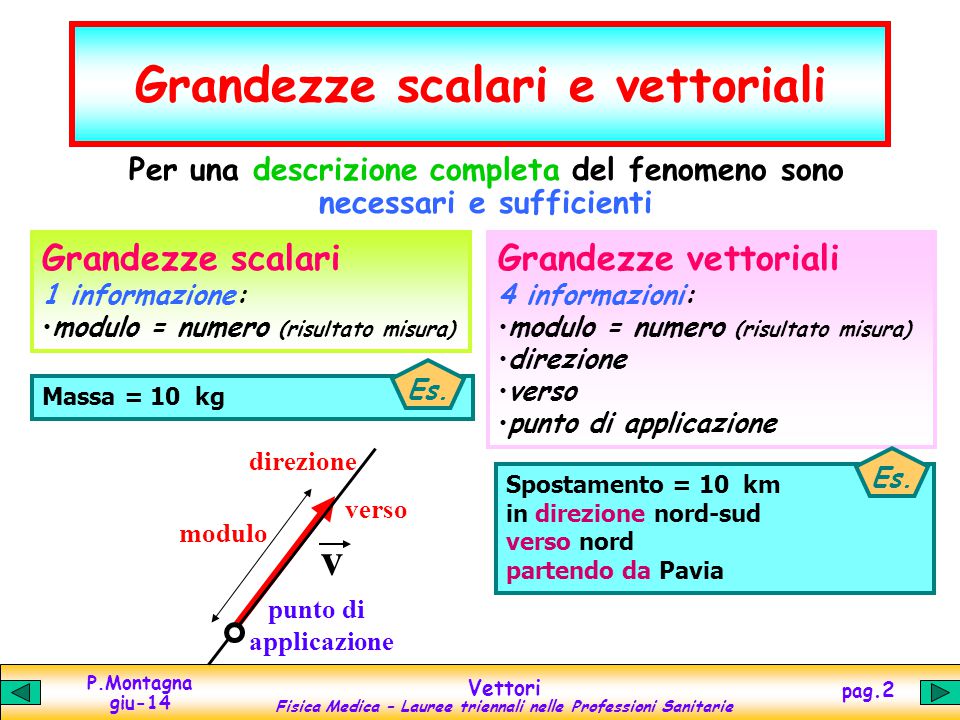
Una grandezza scalare è completamente definita dal suo valore numerico (la sua intensità) e dall'unità di misura. Non ha bisogno di una direzione o un verso per essere compresa. Pensa a:
- La temperatura: 25°C è una temperatura ben definita. Non ha senso parlare di "temperatura verso nord".
- La massa: 5 kg di farina è una quantità ben definita, indipendentemente dalla sua posizione.
- Il tempo: 10 secondi sono un intervallo temporale preciso. Non c'è una "direzione del tempo".
- L'energia: 100 Joule rappresentano una quantità di energia, senza bisogno di specificare una direzione.
- La distanza: 5 metri rappresentano uno spazio percorso.
Le grandezze scalari possono essere sommate e sottratte algebricamente, seguendo le normali regole dell'aritmetica. Ad esempio, se aggiungi 2 kg di mele a 3 kg di pere, ottieni 5 kg di frutta.
Grandezze Vettoriali: Valore, Direzione e Verso
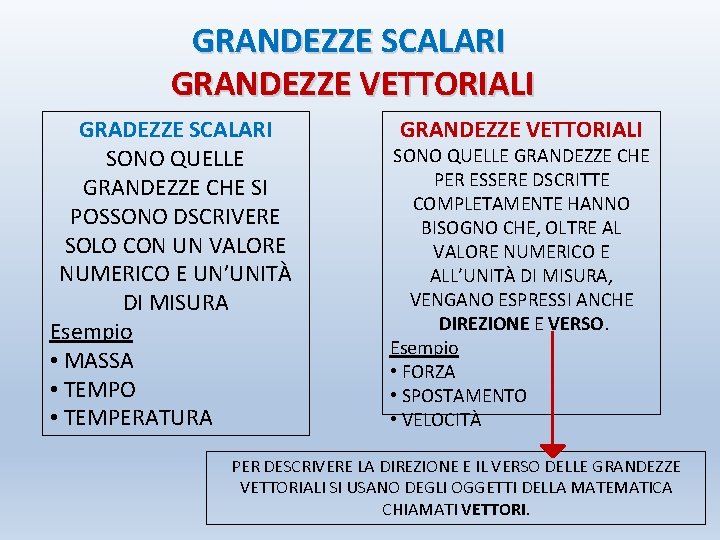
Una grandezza vettoriale, al contrario, richiede per essere completamente definita, oltre al valore numerico (modulo o intensità) e all'unità di misura, anche una direzione e un verso.
- La velocità: Dire che un'auto si muove a 80 km/h non è sufficiente. Dobbiamo anche specificare la direzione (es. "verso nord") e il verso (es. "allontanandosi da Roma").
- La forza: Applicare una forza di 10 Newton a un oggetto richiede di specificare dove viene applicata la forza (la direzione) e in che senso viene spinta o tirata (il verso).
- Lo spostamento: Spostarsi di 5 metri a est è diverso da spostarsi di 5 metri a ovest. La direzione e il verso sono cruciali.
- L'accelerazione: L'accelerazione di un oggetto è la variazione della sua velocità nel tempo. Ha quindi una direzione e un verso.
- Il campo magnetico: Il campo magnetico esercita una forza su cariche in movimento, con una direzione e un verso specifici.
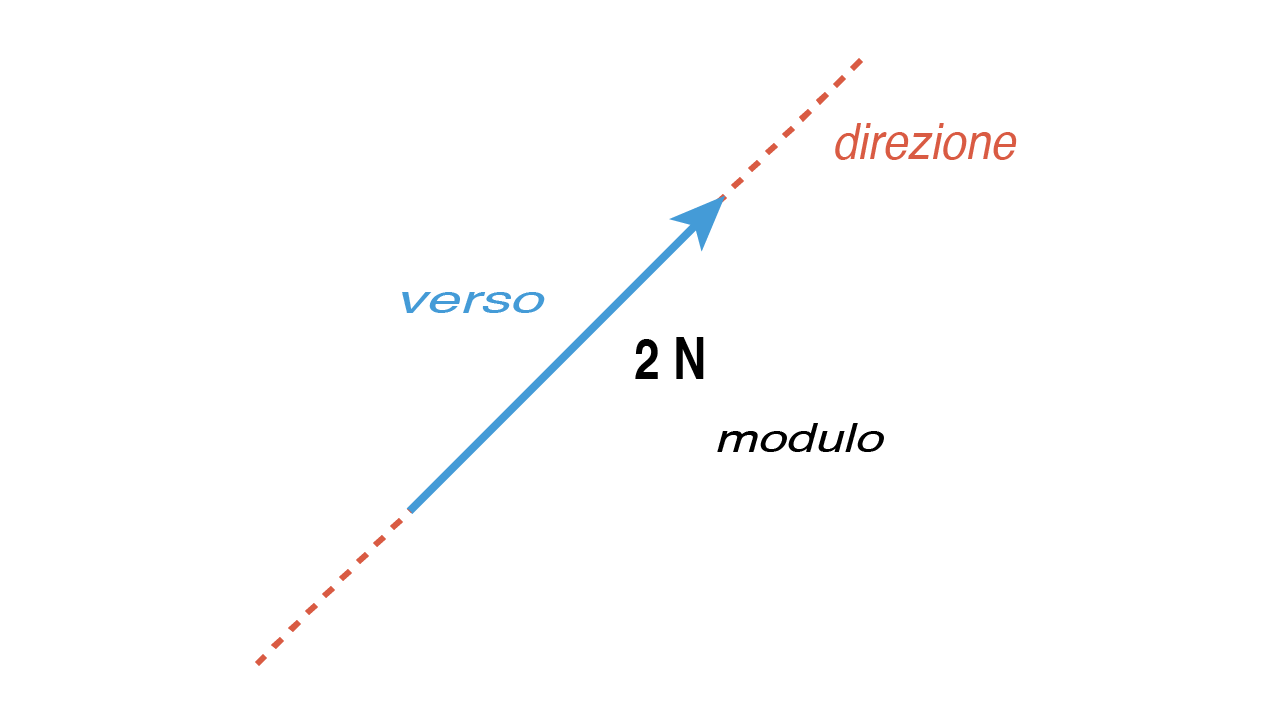
Rappresentazione dei Vettori
I vettori vengono rappresentati graficamente con frecce. La lunghezza della freccia rappresenta il modulo del vettore, la direzione della freccia indica la direzione del vettore e la punta della freccia indica il verso.
Operazioni con i Vettori
A differenza delle grandezze scalari, le grandezze vettoriali non si sommano e sottraggono semplicemente. Per sommare vettori, si usano metodi grafici (come il metodo punta-coda o il metodo del parallelogramma) o metodi analitici (scomponendo i vettori nelle loro componenti). La sottrazione di vettori è equivalente alla somma di un vettore con il vettore opposto (stesso modulo, stessa direzione, verso opposto).
Esempi Concreti: Rendiamolo Relatabile
Immagina di spingere un carrello della spesa. La forza che applichi è una grandezza vettoriale. Non basta sapere quanti Newton stai applicando, ma anche in che direzione e verso stai spingendo il carrello. Se spingi verso il basso, il carrello non si muoverà in avanti!
Quando guidi l'auto, la tua velocità è una grandezza vettoriale. Sapere che stai andando a 90 km/h non dice nulla su dove stai andando. Devi specificare la direzione (es. "verso Milano") e il verso (es. "allontanandosi da Bologna").
Pensa a un GPS. Il GPS ti fornisce la tua posizione (coordinate), la tua velocità e la tua direzione. Senza la direzione, il GPS sarebbe inutile!
Perché è Importante Distinguere tra Scalari e Vettori?
La distinzione tra grandezze scalari e vettoriali è fondamentale in fisica perché influenza il modo in cui queste grandezze interagiscono tra loro e come vengono utilizzate nei calcoli. Ignorare la natura vettoriale di una grandezza può portare a risultati errati.
Ad esempio, in fisica, il lavoro è definito come il prodotto scalare tra la forza e lo spostamento: L = F · s. Se calcolassimo il lavoro come il semplice prodotto del modulo della forza per il modulo dello spostamento, senza considerare l'angolo tra i due vettori, otterremmo un risultato sbagliato. Il lavoro compiuto è massimo quando la forza e lo spostamento hanno la stessa direzione e verso, ed è nullo quando sono perpendicolari.

Un altro esempio è il calcolo della quantità di moto, definita come il prodotto della massa (scalare) per la velocità (vettoriale): p = m · v. La quantità di moto è una grandezza vettoriale e la sua direzione e verso coincidono con quelli della velocità.
In Sintesi: Tabella Comparativa
Per riassumere, ecco una tabella che confronta le grandezze scalari e vettoriali:
Tabella Comparativa
| Caratteristica | Grandezza Scalare | Grandezza Vettoriale |
|---|---|---|
| Definizione | Definita da valore numerico (modulo) e unità di misura. | Definita da valore numerico (modulo), unità di misura, direzione e verso. |
| Esempi | Temperatura, massa, tempo, energia, distanza. | Velocità, forza, spostamento, accelerazione, campo magnetico. |
| Operazioni | Somma e sottrazione algebrica. | Somma e sottrazione vettoriale (metodi grafici o analitici). |
| Rappresentazione | Numero. | Freccia (vettore). |
Conclusione: Un Passo Avanti nella Comprensione del Mondo
Comprendere la differenza tra grandezze scalari e vettoriali è un passo fondamentale per interpretare e descrivere il mondo che ci circonda in modo più accurato. Che tu stia studiando fisica a scuola o semplicemente cercando di capire meglio i fenomeni naturali, questa distinzione ti aiuterà a pensare in modo più critico e a risolvere problemi in modo più efficace. Ricorda, la fisica è ovunque, e imparare a "parlare la sua lingua" ti aprirà un mondo di nuove prospettive. Ora, la prossima volta che sentirai parlare di velocità o forza, saprai esattamente di cosa si tratta e perché la direzione è importante! Speriamo che questo articolo ti sia stato utile e ti abbia fornito una solida base per approfondire ulteriormente le tue conoscenze.