
Capita a tutti noi, a volte, di trovarci di fronte a problemi di geometria che sembrano insormontabili. Magari stai aiutando tuo figlio con i compiti, o forse hai bisogno di calcolare qualcosa per un progetto di bricolage a casa. E improvvisamente ti imbatti in un triangolo isoscele e devi calcolarne la base. Niente panico! Non sei solo. Molti si bloccano di fronte a questo tipo di problemi. La buona notizia è che trovare la base di un triangolo isoscele è più semplice di quanto possa sembrare, una volta compresi i concetti chiave.
In questo articolo, ti guiderò passo dopo passo attraverso diversi metodi per calcolare la base di un triangolo isoscele, rendendo il processo il più chiaro e comprensibile possibile. Cercheremo di evitare tecnicismi eccessivi e di concentrarci su esempi pratici. L'obiettivo è che tu possa acquisire la sicurezza necessaria per affrontare qualsiasi problema che coinvolga triangoli isosceli.
Perché Dovresti Sapere Come Calcolare la Base di un Triangolo Isoscele?
Potresti pensare: "Quando mai mi servirà calcolare la base di un triangolo isoscele nella vita reale?". In realtà, le applicazioni sono molteplici e spesso insospettabili. Ecco alcuni esempi:
- Architettura e Design: Gli architetti utilizzano i triangoli isosceli per progettare tetti, ponti e altre strutture. Conoscere le proprietà di questi triangoli è fondamentale per garantire la stabilità e l'estetica delle costruzioni.
- Falegnameria e Bricolage: Se stai costruendo un mobile, un ripiano o qualsiasi altra struttura in legno, potresti aver bisogno di tagliare dei pezzi a forma di triangolo isoscele. Calcolare la base ti aiuterà a ottenere le dimensioni corrette.
- Navigazione: I triangoli isosceli sono utilizzati in alcuni sistemi di navigazione per calcolare distanze e angoli.
- Matematica e Fisica: Anche se non te ne rendi conto, le basi della geometria, inclusi i triangoli isosceli, sono fondamentali per comprendere concetti più avanzati in matematica e fisica.
In sostanza, la capacità di comprendere e manipolare le proprietà dei triangoli isosceli può tornare utile in una varietà di situazioni, sia professionali che personali. Ti permette di sviluppare il pensiero logico e la capacità di risolvere problemi, competenze preziose in qualsiasi ambito.
Cos'è un Triangolo Isoscele?
Prima di addentrarci nei metodi di calcolo, è importante chiarire cosa intendiamo per triangolo isoscele. Un triangolo isoscele è un triangolo che ha due lati congruenti (cioè della stessa lunghezza). L'angolo compreso tra i due lati congruenti è chiamato angolo al vertice, mentre il lato opposto all'angolo al vertice è chiamato base. Gli angoli adiacenti alla base sono congruenti e sono chiamati angoli alla base.
Proprietà Chiave dei Triangoli Isosceli:
- Due lati sono congruenti.
- Due angoli (gli angoli alla base) sono congruenti.
- L'altezza relativa alla base divide il triangolo in due triangoli rettangoli congruenti. Questa altezza è anche mediana e bisettrice dell'angolo al vertice.
Queste proprietà sono fondamentali per calcolare la base. Le utilizzeremo nei diversi metodi che vedremo a breve.
Metodi per Calcolare la Base di un Triangolo Isoscele
Esistono diversi modi per calcolare la base di un triangolo isoscele, a seconda delle informazioni che hai a disposizione. Vediamone alcuni:
1. Conoscendo l'Altezza e un Lato Obliquo (Uguale)
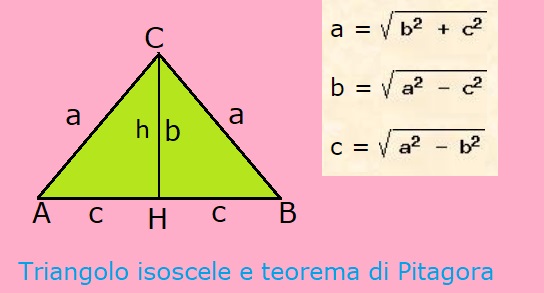
Questo è uno dei metodi più comuni. Utilizziamo il teorema di Pitagora. Ricorda che l'altezza relativa alla base divide il triangolo isoscele in due triangoli rettangoli congruenti. In ciascuno di questi triangoli rettangoli:
- L'ipotenusa è uno dei lati obliqui del triangolo isoscele (l).
- Un cateto è l'altezza del triangolo isoscele (h).
- L'altro cateto è metà della base (b/2).
Il teorema di Pitagora afferma che: a2 + b2 = c2, dove a e b sono i cateti e c è l'ipotenusa. Nel nostro caso, possiamo scrivere:
(b/2)2 + h2 = l2
Risolvendo per b/2, otteniamo:
b/2 = √(l2 - h2)
Quindi, la base b è:
b = 2 * √(l2 - h2)
Esempio: Supponiamo che un lato obliquo di un triangolo isoscele misuri 10 cm e l'altezza misuri 8 cm. Qual è la lunghezza della base?
b = 2 * √(102 - 82) = 2 * √(100 - 64) = 2 * √36 = 2 * 6 = 12 cm
Quindi, la base del triangolo isoscele è di 12 cm.
2. Conoscendo l'Area e l'Altezza
L'area di un triangolo è data dalla formula: Area = (base * altezza) / 2. Se conosciamo l'area (A) e l'altezza (h) del triangolo isoscele, possiamo ricavare la base (b) come segue:
A = (b * h) / 2
Moltiplicando entrambi i lati per 2, otteniamo:
2A = b * h

Dividendo entrambi i lati per h, otteniamo:
b = 2A / h
Esempio: Supponiamo che l'area di un triangolo isoscele sia di 48 cm2 e l'altezza sia di 8 cm. Qual è la lunghezza della base?
b = (2 * 48) / 8 = 96 / 8 = 12 cm
Quindi, la base del triangolo isoscele è di 12 cm.
3. Conoscendo un Lato Obliquo e l'Angolo al Vertice
Questo metodo richiede l'utilizzo della trigonometria. Chiamiamo l'angolo al vertice θ (theta) e la lunghezza di un lato obliquo l. Possiamo dividere il triangolo isoscele in due triangoli rettangoli congruenti, come abbiamo fatto nel primo metodo. In questo caso, l'angolo al vertice viene diviso a metà (θ/2). Possiamo usare la funzione seno per trovare metà della base:
sin(θ/2) = (b/2) / l
Moltiplicando entrambi i lati per l, otteniamo:
b/2 = l * sin(θ/2)
Quindi, la base b è:
b = 2 * l * sin(θ/2)
Esempio: Supponiamo che un lato obliquo di un triangolo isoscele misuri 10 cm e l'angolo al vertice sia di 60 gradi. Qual è la lunghezza della base?
b = 2 * 10 * sin(60/2) = 2 * 10 * sin(30) = 2 * 10 * 0.5 = 10 cm
Quindi, la base del triangolo isoscele è di 10 cm. (In questo caso specifico, il triangolo è anche equilatero poiché tutti i lati sono uguali.)
4. Conoscendo un Lato Obliquo e un Angolo alla Base
Anche in questo caso, utilizziamo la trigonometria. Chiamiamo l'angolo alla base α (alfa) e la lunghezza di un lato obliquo l. Ricordiamo che la somma degli angoli interni di un triangolo è sempre 180 gradi. Quindi, l'angolo al vertice θ è dato da:
θ = 180° - 2α
Una volta calcolato l'angolo al vertice, possiamo usare il metodo precedente (conoscendo un lato obliquo e l'angolo al vertice) per trovare la base.
b = 2 * l * sin(θ/2) = 2 * l * sin((180° - 2α)/2) = 2 * l * sin(90° - α)

Poiché sin(90° - α) = cos(α), possiamo semplificare ulteriormente:
b = 2 * l * cos(α)
Esempio: Supponiamo che un lato obliquo di un triangolo isoscele misuri 10 cm e un angolo alla base sia di 45 gradi. Qual è la lunghezza della base?
b = 2 * 10 * cos(45°) = 2 * 10 * (√2 / 2) = 10√2 cm ≈ 14.14 cm
Quindi, la base del triangolo isoscele è di circa 14.14 cm.
Contro-argomentazioni e Considerazioni
Alcuni potrebbero obiettare che questi metodi sono troppo teorici e difficili da applicare nella pratica. È vero che a volte le misure non sono perfette e che potrebbero esserci degli errori di misurazione. Tuttavia, questi metodi forniscono un'approssimazione accurata della base, che è sufficiente nella maggior parte delle situazioni pratiche. Inoltre, l'uso di strumenti di misurazione precisi e software di geometria può aiutare a ridurre gli errori.
Un'altra obiezione potrebbe essere che esistono calcolatrici online o app che possono calcolare la base automaticamente. Questo è vero, ma è importante capire i concetti alla base del calcolo. Affidarsi ciecamente a una calcolatrice senza comprendere il processo può limitare la tua capacità di risolvere problemi in situazioni in cui non hai accesso a uno strumento di calcolo.
Riepilogo e Conclusione
Abbiamo visto diversi metodi per calcolare la base di un triangolo isoscele, a seconda delle informazioni disponibili. Ricorda che la chiave è comprendere le proprietà fondamentali dei triangoli isosceli e utilizzare il teorema di Pitagora e la trigonometria in modo appropriato.
Speriamo che questo articolo ti abbia fornito gli strumenti necessari per affrontare qualsiasi problema che coinvolga triangoli isosceli. La geometria può sembrare intimidatoria all'inizio, ma con un po' di pratica e pazienza, puoi superare qualsiasi sfida.
Ora, prova ad applicare questi metodi a problemi reali. Prendi un righello, un goniometro e prova a misurare i lati e gli angoli di oggetti a forma di triangolo isoscele che trovi intorno a te. Quanto ti senti più sicuro ora nell'affrontare questi calcoli?