Ciao a tutti! Capisco perfettamente se vi sentite un po' spaesati davanti a un parallelogramma e vi chiedete: "Come trovo l'altezza?" Non preoccupatevi, è una domanda comunissima e una volta compreso il concetto, vi sembrerà tutto molto più semplice. Sono qui per guidarvi passo dopo passo, con un linguaggio chiaro e tanti esempi pratici. Ricordate, la matematica è come un puzzle: ogni pezzo si incastra alla perfezione e, con la giusta guida, possiamo risolverlo insieme!
Cos'è un Parallelogramma e Perché l'Altezza è Importante?
Innanzitutto, rinfreschiamo la memoria. Un parallelogramma è una figura geometrica a quattro lati (un quadrilatero) con lati opposti paralleli e uguali. Pensate a un rettangolo che è stato "spinto" di lato: ecco, quello è un parallelogramma! I rettangoli, i quadrati e i rombi sono tutti casi speciali di parallelogrammi.
L'altezza di un parallelogramma è la distanza perpendicolare tra un lato (chiamato base) e il lato opposto. Non è uno dei lati obliqui! È una linea retta che forma un angolo di 90 gradi (un angolo retto) con la base. L'altezza è fondamentale perché ci serve per calcolare l'area del parallelogramma, che è semplicemente base per altezza.
Come dice spesso la professoressa Rossi, insegnante di matematica delle scuole medie con 20 anni di esperienza, "L'altezza è la chiave per sbloccare l'area! Senza l'altezza, non possiamo sapere quanto spazio occupa la figura." Ecco perché è così importante saperla trovare.
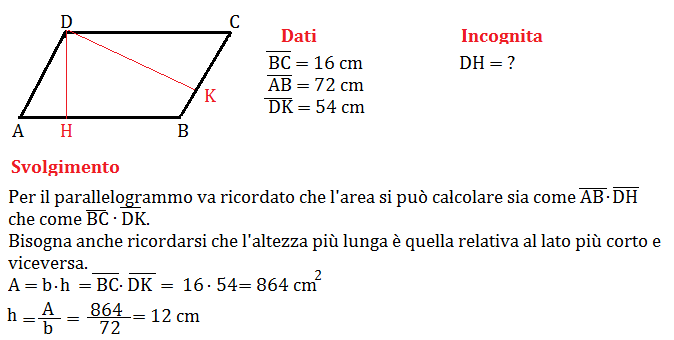
Metodo 1: Conoscendo l'Area e la Base
Questo è il metodo più diretto. Se vi viene fornita l'area (A) del parallelogramma e la lunghezza della base (b), potete calcolare l'altezza (h) utilizzando la seguente formula:
h = A / b
In pratica, dividete l'area per la base. Facile, no?
Esempio: Immaginate di avere un parallelogramma con un'area di 30 cm² e una base di 6 cm. Per trovare l'altezza, dovete dividere 30 cm² per 6 cm. Il risultato è 5 cm. Quindi, l'altezza del parallelogramma è di 5 cm.
Esercizio: Un parallelogramma ha un'area di 48 m² e una base di 8 m. Qual è la sua altezza?

Metodo 2: Utilizzando il Teorema di Pitagora (Se Conosciamo un Lato Obliquo e un Angolo)
Questo metodo è un po' più avanzato e richiede la conoscenza del Teorema di Pitagora. Funziona quando conoscete la lunghezza di un lato obliquo e l'angolo che questo lato forma con la base (o, equivalentemente, la distanza orizzontale tra il punto finale del lato obliquo e l'inizio della base).
Immaginate di "tagliare" il parallelogramma in un punto tale da formare un triangolo rettangolo. L'altezza del parallelogramma corrisponde a uno dei cateti del triangolo, mentre il lato obliquo del parallelogramma diventa l'ipotenusa del triangolo. La parte di base rimanente è l'altro cateto.
Se conoscete la lunghezza del lato obliquo (l'ipotenusa, chiamiamola "c") e la distanza tra il punto finale del lato obliquo e l'inizio della base (un cateto, chiamiamolo "a"), potete trovare l'altezza (l'altro cateto, "b") utilizzando il Teorema di Pitagora:
c² = a² + b²
Per trovare l'altezza (b), dobbiamo riarrangiare la formula:
b² = c² - a²

E infine:
b = √(c² - a²)
Esempio: Un parallelogramma ha un lato obliquo di 5 cm e la distanza orizzontale tra il punto finale del lato obliquo e l'inizio della base è di 3 cm. Per trovare l'altezza, calcoliamo: √(5² - 3²) = √(25 - 9) = √16 = 4 cm. Quindi, l'altezza del parallelogramma è di 4 cm.
Esercizio: Un parallelogramma ha un lato obliquo di 13 m e la distanza orizzontale tra il punto finale del lato obliquo e l'inizio della base è di 5 m. Qual è la sua altezza?
Usando la Trigonometria (Seno dell'Angolo)
Se invece della distanza orizzontale conosci l'angolo (θ) tra la base e il lato obliquo (lato di lunghezza 'c'), puoi usare la trigonometria. In particolare, il seno dell'angolo (sin(θ)) è il rapporto tra l'altezza (h) e il lato obliquo (c):
sin(θ) = h / c

Quindi, per trovare l'altezza (h), usiamo:
h = c * sin(θ)
Assicurati che la tua calcolatrice sia impostata sulla modalità corretta (gradi o radianti) a seconda di come ti è stato dato l'angolo.
Esempio: Un parallelogramma ha un lato obliquo di 10 cm e l'angolo tra il lato obliquo e la base è di 30 gradi. Il seno di 30 gradi è 0.5. Quindi, l'altezza è 10 cm * 0.5 = 5 cm.
Esercizio: Un parallelogramma ha un lato obliquo di 8 m e l'angolo tra il lato obliquo e la base è di 45 gradi. Qual è la sua altezza (sin(45°) ≈ 0.707)?
Metodo 3: Utilizzando le Coordinate dei Vertici
Questo metodo è più avanzato e richiede la conoscenza della geometria analitica. Se conoscete le coordinate dei vertici del parallelogramma, potete utilizzare formule specifiche per calcolare la distanza tra un punto (un vertice) e una retta (il lato opposto). Questa distanza è l'altezza.
Tuttavia, questo metodo è generalmente più complesso e viene utilizzato in contesti più avanzati. Non mi dilungherò troppo qui, ma sappiate che è un'opzione valida se vi trovate in questa situazione.
Consigli Utili e Trucchi
- Disegnate sempre un diagramma! Visualizzare il problema vi aiuterà a capire meglio le relazioni tra le diverse parti del parallelogramma.
- Assicuratevi di usare le unità di misura corrette. Se la base è in centimetri, l'altezza deve essere anch'essa in centimetri. L'area sarà quindi in centimetri quadrati.
- Controllate sempre il vostro lavoro. Un piccolo errore può portare a un risultato sbagliato.
- Non abbiate paura di chiedere aiuto! Se siete bloccati, chiedete al vostro insegnante, a un tutor o a un compagno di classe.
- Praticate, praticate, praticate! Più esercizi fate, più facile diventerà trovare l'altezza di un parallelogramma.
Come afferma il Dott. Bianchi, un rinomato matematico: "La pratica costante è fondamentale per padroneggiare qualsiasi concetto matematico. Non scoraggiatevi di fronte alle difficoltà, ma consideratele come opportunità di crescita."
Applicazioni Pratiche nella Vita Quotidiana
Potreste chiedervi: "Ma a cosa mi serve sapere come trovare l'altezza di un parallelogramma nella vita reale?". In realtà, ci sono diverse applicazioni pratiche:
- Architettura e Ingegneria: I parallelogrammi vengono utilizzati nella progettazione di edifici, ponti e altre strutture. Calcolare l'area di una superficie a forma di parallelogramma è fondamentale per determinare la quantità di materiali necessari.
- Design: I parallelogrammi possono essere utilizzati in design grafico e nella creazione di motivi geometrici.
- Giardinaggio: Se dovete calcolare l'area di un'aiuola a forma di parallelogramma per sapere quanta terra vi serve.
- Arte: Molti artisti utilizzano parallelogrammi nelle loro opere, sia consapevolmente che inconsciamente.
Attività per Mettere in Pratica le Tue Conoscenze
Ecco alcune attività per consolidare ciò che avete imparato:
- Disegnate diversi parallelogrammi su un foglio di carta. Misurate la base e l'altezza di ciascun parallelogramma e calcolate l'area.
- Cercate oggetti a forma di parallelogramma nella vostra casa o nel vostro quartiere. Provate a stimare l'area di questi oggetti.
- Create un puzzle geometrico utilizzando parallelogrammi di diverse dimensioni.
- Giocate online a giochi di matematica che coinvolgono i parallelogrammi. Ce ne sono tantissimi disponibili!
Conclusione
Spero che questa guida vi sia stata utile per capire come trovare l'altezza di un parallelogramma. Ricordate, la chiave del successo è la comprensione dei concetti e la pratica costante. Non abbiate paura di sperimentare, di fare errori e di imparare da essi. La matematica può essere divertente e gratificante se affrontata con la giusta mentalità. Credete in voi stessi e nelle vostre capacità!
Ora tocca a voi! Prendete carta e penna e mettetevi alla prova con gli esercizi proposti. Sono sicuro che sarete in grado di risolvere qualsiasi problema. Buon lavoro!