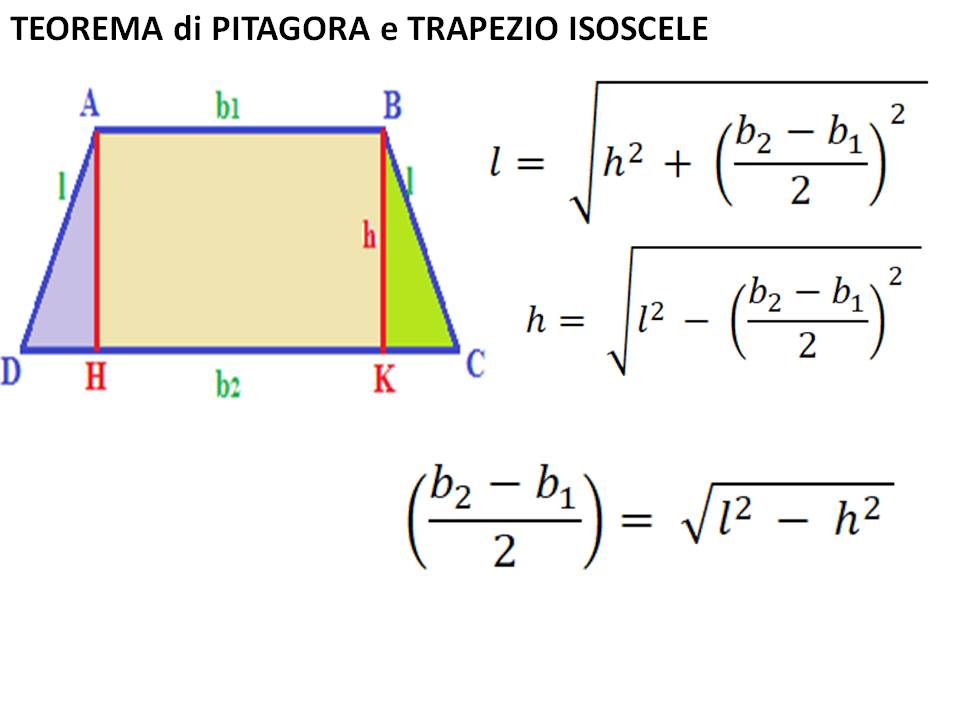
L'altezza di un trapezio isoscele è un segmento perpendicolare che congiunge le due basi parallele, la base maggiore e la base minore. Comprendere come calcolarla è fondamentale per risolvere problemi geometrici e applicazioni pratiche.
Definizione e Importanza dell'Altezza nel Trapezio Isoscele
Nel contesto della geometria, l'altezza di un trapezio isoscele rappresenta la distanza tra le sue basi. A differenza di un trapezio scaleno, il trapezio isoscele possiede due lati obliqui congruenti, il che semplifica alcuni calcoli. L'altezza è cruciale perché permette di calcolare l'area del trapezio e di applicare il teorema di Pitagora per determinare le lunghezze dei lati.
La conoscenza del metodo per calcolare l'altezza è essenziale per gli studenti di matematica, poiché si tratta di un concetto che si ripresenta in diverse aree, dalla geometria piana alla trigonometria. La capacità di manipolare formule e risolvere problemi relativi ai trapezi isosceli contribuisce allo sviluppo del pensiero critico e delle abilità di problem-solving.
Metodi per Calcolare l'Altezza
Esistono diversi approcci per determinare l'altezza di un trapezio isoscele, a seconda delle informazioni disponibili.
1. Conoscendo le Basi e i Lati Obliqui
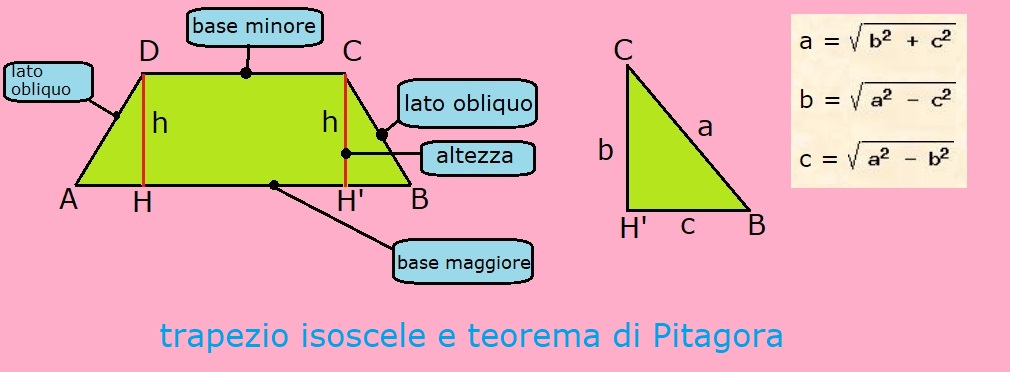
Se conosciamo la lunghezza delle basi (B, base maggiore e b, base minore) e la lunghezza dei lati obliqui (l), possiamo utilizzare il teorema di Pitagora. Si traccia l'altezza da un vertice della base minore alla base maggiore. Questo crea un triangolo rettangolo il cui cateto è l'altezza del trapezio, l'ipotenusa è il lato obliquo, e l'altro cateto è pari a (B - b) / 2.
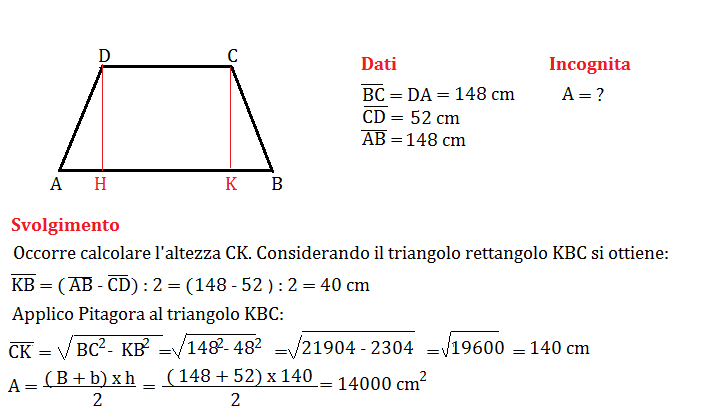
Quindi, l'altezza (h) si calcola con la formula:
h = √(l² - ((B - b) / 2)²)
2. Conoscendo l'Area e le Basi
Se l'area (A) del trapezio e la lunghezza delle basi sono note, possiamo utilizzare la formula dell'area del trapezio per ricavare l'altezza:
A = ((B + b) / 2) * h
Risolvendo per h, otteniamo:
h = (2 * A) / (B + b)
3. Utilizzando la Trigonometria
Se conosciamo l'angolo che un lato obliquo forma con la base maggiore (θ) e la lunghezza del lato obliquo (l), possiamo utilizzare le funzioni trigonometriche. L'altezza è il cateto opposto all'angolo θ nel triangolo rettangolo formato. Pertanto:

h = l * sin(θ)
Applicazioni Pratiche
La comprensione del calcolo dell'altezza del trapezio isoscele non è solo un esercizio teorico. Trova applicazioni pratiche in diversi contesti. Ad esempio:
- Architettura e Ingegneria: Nel progettare tetti, ponti o altre strutture che presentano forme trapezoidali, è fondamentale calcolare correttamente le dimensioni, inclusa l'altezza.
- Geometria Descrittiva: La rappresentazione di oggetti tridimensionali su un piano richiede la conoscenza delle proprietà geometriche delle figure, inclusi i trapezi.
- Vita Quotidiana: Anche in situazioni comuni, come il calcolo della superficie di un terreno con una forma simile a un trapezio, la conoscenza della formula dell'area e del metodo per calcolare l'altezza può essere utile.
Ricerca e Didattica: Numerosi studi pedagogici sottolineano l'importanza di un approccio pratico all'insegnamento della geometria. Secondo Piaget, l'apprendimento è più efficace quando gli studenti sono attivamente coinvolti nella risoluzione di problemi concreti. Pertanto, l'applicazione dei concetti geometrici a situazioni reali favorisce una comprensione più profonda e duratura.
In conclusione, il calcolo dell'altezza del trapezio isoscele è una competenza fondamentale per gli studenti. La padronanza di questo concetto non solo rafforza le basi della geometria, ma apre anche la strada a una comprensione più ampia delle applicazioni pratiche della matematica nel mondo che ci circonda.