Il trapezio, una figura geometrica con quattro lati di cui due paralleli, è una forma che incontriamo frequentemente sia in contesti matematici che nel mondo reale. Comprendere come calcolare le sue dimensioni, in particolare la base maggiore, è fondamentale per diverse applicazioni pratiche. Questo articolo esplorerà in dettaglio i metodi per trovare la base maggiore di un trapezio, fornendo una guida chiara e completa.
Comprendere il Trapezio: Definizioni e Proprietà
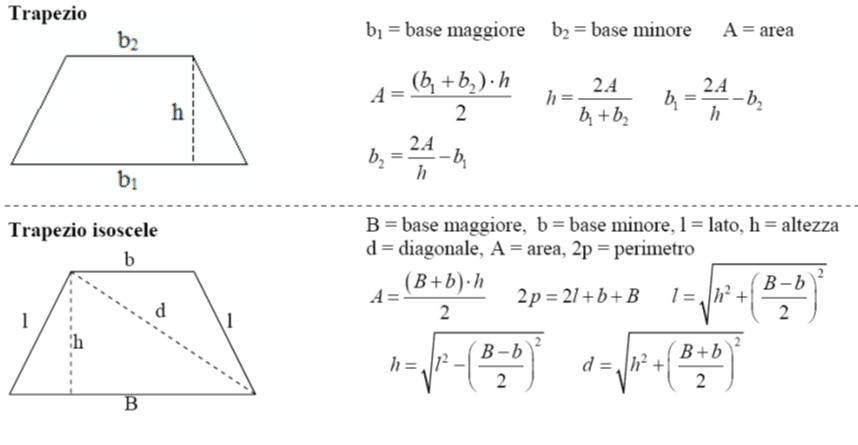
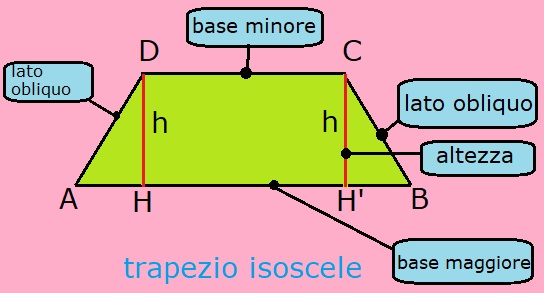
Prima di addentrarci nei calcoli, è essenziale definire con precisione cos'è un trapezio e quali sono le sue proprietà principali. Un trapezio è un quadrilatero con due lati paralleli, chiamati basi, e due lati non paralleli. La base più lunga è definita come la base maggiore (B), mentre la base più corta è la base minore (b). L'altezza (h) è la distanza perpendicolare tra le due basi. I lati non paralleli sono spesso chiamati lati obliqui.
Tipi di Trapezi
Esistono diverse tipologie di trapezi, ciascuna con caratteristiche specifiche:
- Trapezio Rettangolo: Uno dei lati non paralleli è perpendicolare alle basi, formando due angoli retti.
- Trapezio Isoscele: I lati non paralleli sono congruenti (della stessa lunghezza) e gli angoli alla base sono uguali.
- Trapezio Scaleno: Tutti i lati e gli angoli sono diversi.
La tipologia di trapezio influenza il metodo più appropriato per calcolare la base maggiore, sebbene i principi fondamentali rimangano gli stessi.
Metodi per Trovare la Base Maggiore
Esistono diversi approcci per determinare la lunghezza della base maggiore di un trapezio, a seconda delle informazioni disponibili. Analizzeremo i metodi più comuni:
1. Conoscendo l'Area, l'Altezza e la Base Minore
Se conosciamo l'area (A) del trapezio, l'altezza (h) e la base minore (b), possiamo utilizzare la formula dell'area del trapezio per ricavare la base maggiore (B):
A = (B + b) * h / 2
Per trovare B, dobbiamo manipolare l'equazione:
2A = (B + b) * h
2A / h = B + b
B = (2A / h) - b
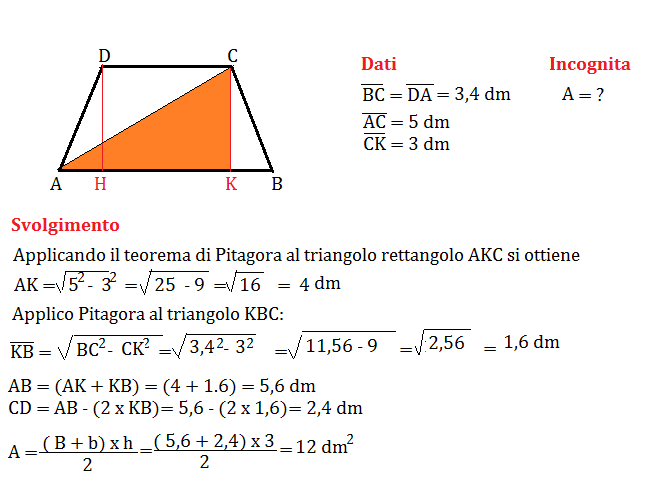
Esempio: Supponiamo che un trapezio abbia un'area di 50 cm², un'altezza di 5 cm e una base minore di 6 cm. Applicando la formula, otteniamo:
B = (2 * 50 / 5) - 6 = (100 / 5) - 6 = 20 - 6 = 14 cm
Quindi, la base maggiore è di 14 cm.
2. Conoscendo l'Altezza, l'Area e la Linea Media
La linea media di un trapezio è il segmento che congiunge i punti medi dei lati non paralleli. La sua lunghezza è la media aritmetica delle lunghezze delle basi:
Linea media = (B + b) / 2
L'area del trapezio può anche essere calcolata come il prodotto della linea media per l'altezza:
A = Linea media * h
Se conosciamo l'area e l'altezza, possiamo trovare la linea media:
Linea media = A / h
Poi, se conosciamo anche la base minore (b), possiamo trovare la base maggiore (B):
B = 2 * Linea media - b
Esempio: Un trapezio ha un'area di 75 cm² e un'altezza di 10 cm. La sua base minore è di 5 cm. La linea media è A/h = 75/10 = 7.5 cm. Quindi, la base maggiore è B = 2 * 7.5 - 5 = 15 - 5 = 10 cm.
3. Utilizzando la Trigonometria (Trapezio Rettangolo o Isoscele)
Nei trapezi rettangoli o isosceli, la trigonometria può essere utile se conosciamo l'angolo tra un lato obliquo e una base e la lunghezza di quel lato obliquo o dell'altezza.
Trapezio Rettangolo: Se conosciamo l'angolo tra il lato obliquo e la base maggiore (α) e la lunghezza del lato obliquo (l), possiamo trovare la differenza tra le basi (B - b) usando:
B - b = l * cos(α)
Se conosciamo anche la base minore (b), possiamo trovare la base maggiore:
B = b + l * cos(α)
In alternativa, se conosciamo l'altezza (h) e l'angolo α, possiamo usare:
B - b = h / tan(α)
B = b + h / tan(α)
Trapezio Isoscele: Il processo è simile, ma dobbiamo considerare che i due lati obliqui sono congruenti e gli angoli alla base sono uguali. Possiamo dividere il trapezio in un rettangolo e due triangoli rettangoli congruenti. Utilizzando le funzioni trigonometriche e le lunghezze appropriate, possiamo calcolare la differenza tra le basi e, quindi, la base maggiore.
4. Utilizzando i Lati Obliqui e l'Altezza
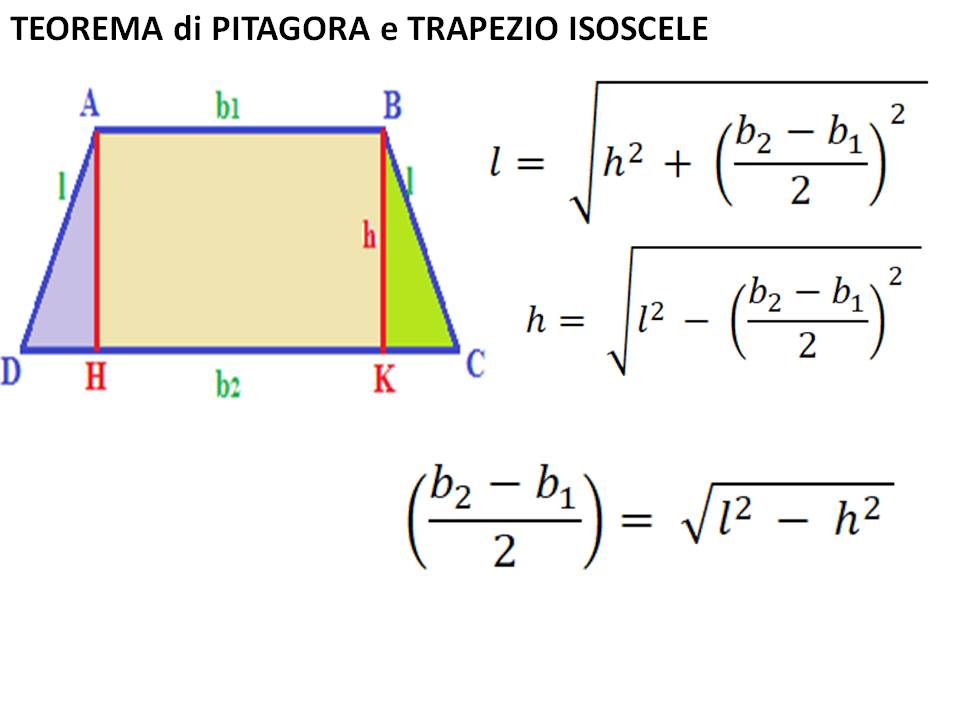
Se conosciamo le lunghezze dei lati obliqui (l1 e l2) e l'altezza (h), possiamo utilizzare il teorema di Pitagora e alcune proprietà geometriche per calcolare la differenza tra le basi (B - b) e quindi, se conosciamo la base minore, la base maggiore.
Immaginiamo di tracciare le altezze dai vertici della base minore alla base maggiore. Questo divide il trapezio in un rettangolo al centro e due triangoli rettangoli ai lati. Chiamiamo le basi di questi triangoli x e y. Allora:
B = b + x + y
Possiamo usare il teorema di Pitagora per trovare x e y:
x = √(l1² - h²)
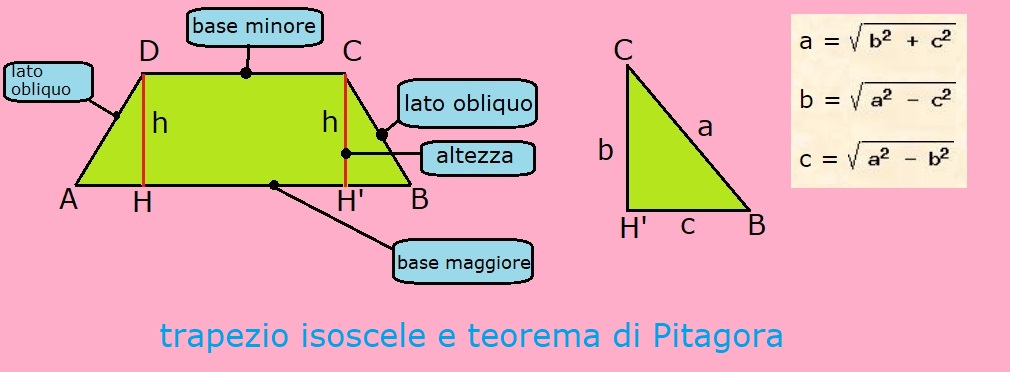
y = √(l2² - h²)
Quindi:
B = b + √(l1² - h²) + √(l2² - h²)
Esempi Pratici e Applicazioni Reali
La capacità di calcolare la base maggiore di un trapezio ha applicazioni pratiche in vari campi:
- Architettura e Ingegneria Civile: Calcolo dell'area di tetti a forma di trapezio, progettazione di ponti e rampe.
- Agricoltura: Stima dell'area di terreni irregolari per la pianificazione delle colture.
- Design e Arti Grafiche: Creazione di elementi grafici con forme trapezoidali precise.
- Geometria e Matematica: Risoluzione di problemi geometrici più complessi che coinvolgono trapezi e altre figure.
Ad esempio, un architetto potrebbe aver bisogno di calcolare l'area di un tetto trapezoidale per stimare la quantità di materiali da costruzione necessari. Un ingegnere civile potrebbe usare questi calcoli per determinare la stabilità di un ponte con sezioni a forma di trapezio.
Consideriamo un campo agricolo a forma di trapezio. Un agricoltore conosce la lunghezza della base minore (50 metri), l'altezza (30 metri) e l'area totale (2400 metri quadrati). Per pianificare le colture in modo efficiente, ha bisogno di conoscere la lunghezza della base maggiore. Utilizzando la formula precedentemente descritta: B = (2A / h) - b = (2 * 2400 / 30) - 50 = (4800 / 30) - 50 = 160 - 50 = 110 metri. Pertanto, la base maggiore del campo è di 110 metri.
Considerazioni Finali
Calcolare la base maggiore di un trapezio richiede una comprensione chiara delle proprietà del trapezio e la selezione del metodo appropriato in base alle informazioni disponibili. La formula dell'area, la trigonometria e il teorema di Pitagora sono strumenti preziosi per risolvere questi problemi.
Ricorda che la precisione nei calcoli è fondamentale, soprattutto in applicazioni pratiche come l'architettura e l'ingegneria. Verifica sempre i tuoi risultati e utilizza unità di misura coerenti.
Speriamo che questa guida completa ti abbia fornito le conoscenze e gli strumenti necessari per affrontare con successo il calcolo della base maggiore di un trapezio. Non esitare a esercitarti con diversi esempi per consolidare la tua comprensione.