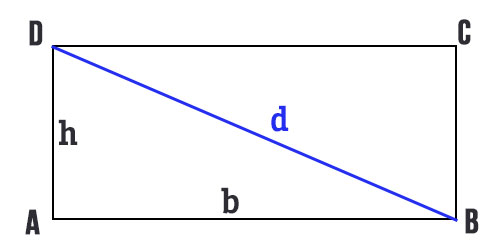
Ciao a tutti! Immagina un rettangolo. Una forma semplice, familiare, quasi una costante nelle nostre vite. La vediamo nei libri, negli schermi dei nostri telefoni, nelle finestre che guardano il mondo. Ma dietro questa apparente semplicità si cela un piccolo tesoro matematico: la sua diagonale.
Calcolare la diagonale di un rettangolo è un'esperienza che va ben oltre la semplice applicazione di una formula. È un invito a esplorare, a connettere concetti, a scoprire la bellezza nascosta in un'equazione. È un piccolo viaggio nel cuore della geometria, un viaggio che arricchisce non solo la nostra conoscenza matematica, ma anche il nostro modo di pensare.
Come si intraprende questo viaggio? Beh, la chiave è un amico fidato: il Teorema di Pitagora. Questo teorema, che porta il nome del grande matematico greco, è un pilastro della geometria, un faro che illumina la relazione tra i lati di un triangolo rettangolo. E indovina un po'? Ogni rettangolo, quando viene tagliato dalla sua diagonale, si trasforma magicamente in due triangoli rettangoli!
Il Teorema di Pitagora: Un Ponte Verso la Soluzione
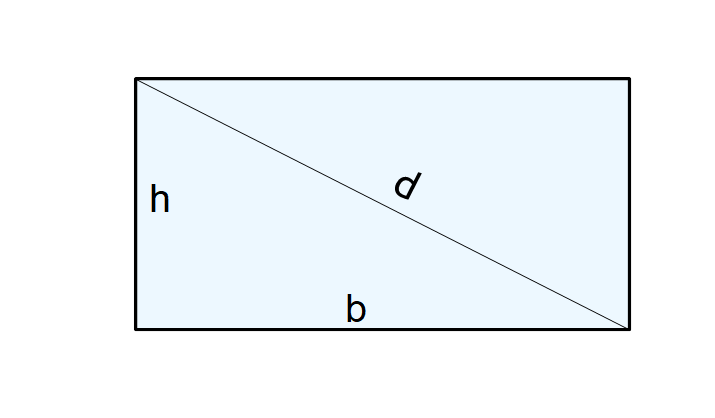
Il Teorema di Pitagora afferma che, in un triangolo rettangolo, il quadrato costruito sull'ipotenusa (il lato opposto all'angolo retto, che nel nostro caso è proprio la diagonale del rettangolo) è uguale alla somma dei quadrati costruiti sui cateti (gli altri due lati, che nel nostro caso sono la base e l'altezza del rettangolo). In termini matematici: a² + b² = c², dove a e b sono i cateti e c è l'ipotenusa.
Quindi, per calcolare la diagonale del nostro rettangolo (che è l'ipotenusa), dobbiamo semplicemente applicare questa formula. Se conosciamo la lunghezza della base (a) e dell'altezza (b) del rettangolo, possiamo calcolare la diagonale (c) come segue:

Passaggi Semplici per un Risultato Brillante
- Eleva al quadrato la lunghezza della base (a²).
- Eleva al quadrato la lunghezza dell'altezza (b²).
- Somma i due risultati (a² + b²).
- Calcola la radice quadrata della somma ottenuta (√(a² + b²)). Il risultato è la lunghezza della diagonale!
Sembra complicato? Forse all'inizio. Ma con un po' di pratica, diventerà un processo naturale, quasi intuitivo. Ricorda, la matematica è come una lingua: più la pratichi, più fluentemente la parli. E ogni problema risolto è una parola nuova che impariamo, una sfumatura in più che aggiungiamo al nostro vocabolario mentale.
Ma c'è di più. Calcolare la diagonale di un rettangolo ci insegna qualcosa di fondamentale: l'importanza della perseveranza. Non sempre la risposta è immediata. A volte dobbiamo sperimentare, provare diverse strade, magari anche commettere qualche errore. Ma è proprio attraverso gli errori che impariamo, che cresciamo, che affiniamo la nostra comprensione del mondo. Pitagora stesso, immagino, non ha scoperto il suo teorema al primo tentativo!
E poi, c'è la bellezza dell'umiltà. La matematica, come la vita, è un viaggio di scoperta continuo. Non importa quanto ne sappiamo, c'è sempre qualcosa di nuovo da imparare, una prospettiva diversa da considerare. Riconoscere i nostri limiti, essere aperti all'apprendimento, è la chiave per una crescita costante.
Infine, non dimentichiamo la curiosità. Chiediamoci sempre "perché?". Perché funziona il Teorema di Pitagora? Quali altre applicazioni ha? La curiosità è il motore dell'apprendimento, la scintilla che accende la nostra passione per la conoscenza.
Quindi, la prossima volta che vedrai un rettangolo, non pensarci solo come a una semplice forma geometrica. Pensa a Pitagora, al suo teorema, alla bellezza nascosta nella matematica. Pensa alla perseveranza, all'umiltà e alla curiosità. E ricorda che ogni problema, per quanto difficile possa sembrare, è un'opportunità per imparare, crescere e scoprire la magia che si cela nel mondo che ci circonda. In bocca al lupo!