Ti sei mai chiesto come calcolare la recinzione ideale per il tuo orto rettangolare, o quanto nastro ti serve per decorare una cornice? Capire come calcolare il perimetro di un rettangolo è un'abilità fondamentale, sorprendentemente utile nella vita di tutti i giorni. Questa guida è pensata per chiunque voglia rinfrescare le proprie conoscenze di geometria, dagli studenti che si preparano per un compito, ai professionisti che devono stimare materiali per un progetto, fino a chi semplicemente vuole capire meglio il mondo che lo circonda.
Cos'è il Perimetro e Perché è Importante?
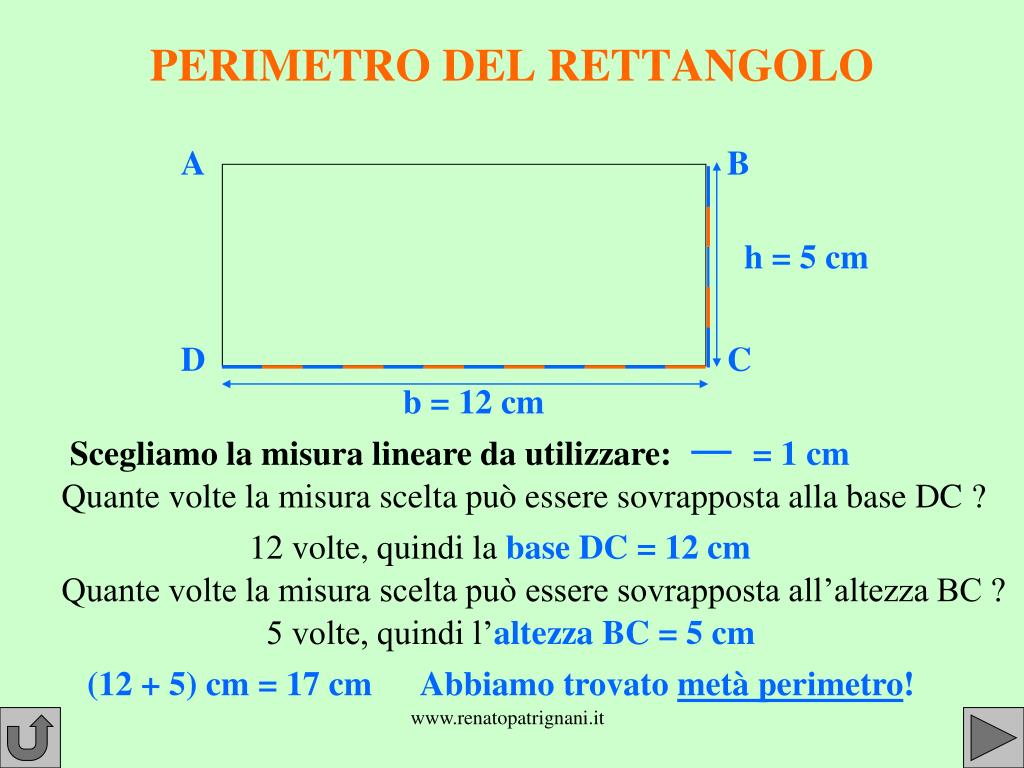
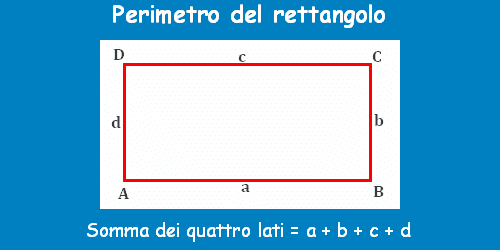
Il perimetro, in termini semplici, è la lunghezza totale del contorno di una figura geometrica. Immagina di dover camminare intorno al tuo giardino: la distanza che percorri è il perimetro del giardino stesso. Nel caso di un rettangolo, il perimetro rappresenta la somma delle lunghezze di tutti i suoi quattro lati.
Comprendere come calcolare il perimetro è essenziale per diverse ragioni:
- Calcolo dei materiali: Sia che tu stia costruendo una recinzione, incorniciando un quadro o cucendo un bordo, sapere il perimetro ti aiuta a stimare la quantità di materiali necessari, evitando sprechi e risparmiando denaro.
- Design e pianificazione: Architetti, designer e ingegneri utilizzano il perimetro per progettare edifici, giardini e altre strutture, assicurandosi che abbiano le dimensioni corrette e si adattino allo spazio disponibile.
- Risoluzione di problemi pratici: Molti problemi di matematica e fisica richiedono la conoscenza del perimetro per essere risolti.
Il Rettangolo: Un Breve Ripasso
Prima di addentrarci nel calcolo, ripassiamo brevemente le caratteristiche di un rettangolo. Un rettangolo è un quadrilatero (una figura con quattro lati) con le seguenti proprietà:
- Quattro angoli retti: Tutti gli angoli di un rettangolo misurano 90 gradi.
- Lati opposti congruenti: I lati opposti di un rettangolo hanno la stessa lunghezza. In altre parole, la base è uguale alla base opposta, e l'altezza è uguale all'altezza opposta.
Grazie a queste proprietà, il calcolo del perimetro di un rettangolo diventa particolarmente semplice.
La Formula Magica: Come Calcolare il Perimetro di un Rettangolo
La formula per calcolare il perimetro di un rettangolo è incredibilmente semplice. Dato che i lati opposti sono uguali, possiamo utilizzare la seguente formula:

Perimetro (P) = 2 * (base + altezza)
Dove:
- base (b) è la lunghezza di uno dei lati più lunghi del rettangolo.
- altezza (h) è la lunghezza di uno dei lati più corti del rettangolo.
In parole povere, sommi la lunghezza della base e dell'altezza, e poi moltiplichi il risultato per 2. Voilà, hai il perimetro!
Esempi Pratici: Mettiamoci al Lavoro!
Per rendere il concetto ancora più chiaro, vediamo alcuni esempi pratici:
Esempio 1: Il Tavolo da Pranzo
Immagina di avere un tavolo da pranzo rettangolare con una base di 180 cm e un'altezza di 90 cm. Qual è il perimetro del tavolo?
- Identifica la base e l'altezza: b = 180 cm, h = 90 cm
- Applica la formula: P = 2 * (180 cm + 90 cm)
- Calcola: P = 2 * (270 cm) = 540 cm
Quindi, il perimetro del tavolo da pranzo è di 540 cm.
Esempio 2: Il Giardino Rettangolare
Vuoi recintare il tuo giardino rettangolare che ha una base di 12 metri e un'altezza di 8 metri. Quanti metri di recinzione ti servono?

- Identifica la base e l'altezza: b = 12 m, h = 8 m
- Applica la formula: P = 2 * (12 m + 8 m)
- Calcola: P = 2 * (20 m) = 40 m
Ti serviranno 40 metri di recinzione per il tuo giardino.
Esempio 3: La Cornice di un Quadro
Stai incorniciando un quadro rettangolare con una base di 30 cm e un'altezza di 20 cm. Quanti centimetri di cornice ti servono?
- Identifica la base e l'altezza: b = 30 cm, h = 20 cm
- Applica la formula: P = 2 * (30 cm + 20 cm)
- Calcola: P = 2 * (50 cm) = 100 cm
Ti serviranno 100 centimetri di cornice per il tuo quadro.

Variazioni e Trucchi Utili
A volte, i problemi potrebbero essere formulati in modo leggermente diverso. Ecco alcuni trucchi per affrontare le variazioni:
- Se conosci il perimetro e un lato: Supponiamo di conoscere il perimetro (P) e la base (b) di un rettangolo. Possiamo ricavare l'altezza (h) riarrangiando la formula: h = (P / 2) - b
- Usa sempre le stesse unità di misura: Assicurati che la base e l'altezza siano espresse nella stessa unità di misura (es. centimetri, metri, pollici) prima di applicare la formula. Se necessario, converti le unità.
Oltre la Teoria: Il Perimetro nella Vita Reale
Il calcolo del perimetro non è solo un esercizio di matematica. È un'abilità pratica che utilizziamo, consciamente o inconsciamente, in molte situazioni quotidiane. Pensiamo a quando dobbiamo:
- Organizzare i mobili in una stanza: Stimare lo spazio disponibile per assicurarsi che i mobili si adattino.
- Pianificare un evento: Calcolare la quantità di festoni o luci necessarie per decorare un'area rettangolare.
- Cucire: Misurare il bordo di una tovaglia o di un lenzuolo per aggiungere un orlo.
Questi sono solo alcuni esempi di come il perimetro si insinua nella nostra vita di tutti i giorni. Comprendere come calcolarlo ci permette di prendere decisioni più informate e risolvere problemi in modo più efficiente.
Conclusione: Il Potere della Geometria
Speriamo che questa guida ti abbia fornito una comprensione chiara e completa di come calcolare il perimetro di un rettangolo. Ricorda, la formula è semplice: P = 2 * (base + altezza). Con un po' di pratica, sarai in grado di applicare questa formula a una vasta gamma di problemi pratici. La geometria, spesso vista come una materia astratta, è in realtà uno strumento potente che ci aiuta a comprendere e interagire con il mondo che ci circonda. Quindi, la prossima volta che ti troverai di fronte a un problema che coinvolge un rettangolo, non esitare: tira fuori la tua formula e mettiti al lavoro!