Capita a tutti di sentirsi un po' spaesati di fronte ai nuovi concetti della matematica, specialmente quando si affronta un argomento come gli insiemi al primo anno del Liceo Scientifico. Non preoccuparti, è del tutto normale! Questo articolo è pensato per aiutarti a superare le difficoltà più comuni e affrontare con successo le verifiche.
Comprendere le Difficoltà Comuni
Molti studenti trovano ostico l'approccio iniziale alla teoria degli insiemi. Alcuni problemi tipici includono:
- Confusione nella terminologia: Simboli come ∈, ⊆, ∪, ∩ possono sembrare geroglifici all'inizio.
- Difficoltà nell'applicazione pratica: Comprendere i concetti teorici ma faticare a risolvere gli esercizi.
- Mancanza di una visualizzazione chiara: Fare fatica ad immaginare gli insiemi e le loro relazioni.
La buona notizia è che questi ostacoli sono superabili con la giusta strategia e un po' di pazienza. Ricorda che, secondo studi sull'apprendimento della matematica (Hiebert & Grouws, 2007), la comprensione concettuale profonda è fondamentale per la successiva applicazione pratica. Non limitarti a memorizzare formule, ma cerca di capire perché funzionano.
Una Guida Pratica allo Studio degli Insiemi
1. Chiarezza nella Terminologia
Il primo passo è padroneggiare il linguaggio degli insiemi. Ecco alcuni termini chiave da conoscere:
- Insieme: Una collezione di oggetti distinti, chiamati elementi.
- Appartenenza (∈): Indica se un elemento fa parte di un insieme. Esempio: 3 ∈ {1, 2, 3} (3 appartiene all'insieme {1, 2, 3}).
- Sottoinsieme (⊆): Un insieme A è un sottoinsieme di un insieme B se ogni elemento di A è anche un elemento di B. Esempio: {1, 2} ⊆ {1, 2, 3}.
- Unione (∪): L'unione di due insiemi A e B è l'insieme che contiene tutti gli elementi di A e tutti gli elementi di B. Esempio: {1, 2} ∪ {3, 4} = {1, 2, 3, 4}.
- Intersezione (∩): L'intersezione di due insiemi A e B è l'insieme che contiene solo gli elementi che appartengono sia ad A che a B. Esempio: {1, 2, 3} ∩ {2, 3, 4} = {2, 3}.
- Insieme Vuoto (∅): Un insieme che non contiene alcun elemento.
Consiglio per gli studenti: Crea un glossario personale con le definizioni e degli esempi per ogni termine. Rivedilo regolarmente.
2. Visualizzazione degli Insiemi: Diagrammi di Venn
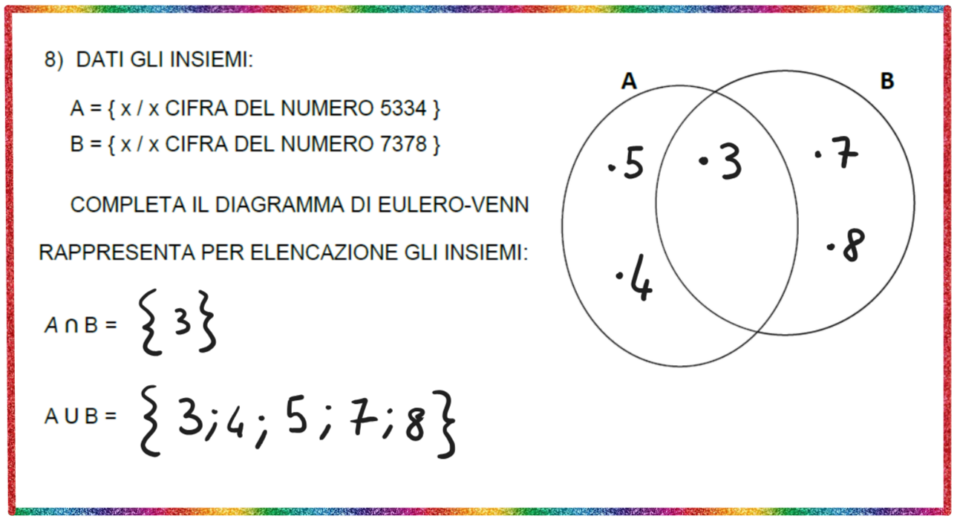
I diagrammi di Venn sono strumenti potentissimi per visualizzare gli insiemi e le loro relazioni. Ogni insieme è rappresentato da un cerchio (o un'altra figura chiusa), e l'area di sovrapposizione tra i cerchi rappresenta l'intersezione tra gli insiemi.
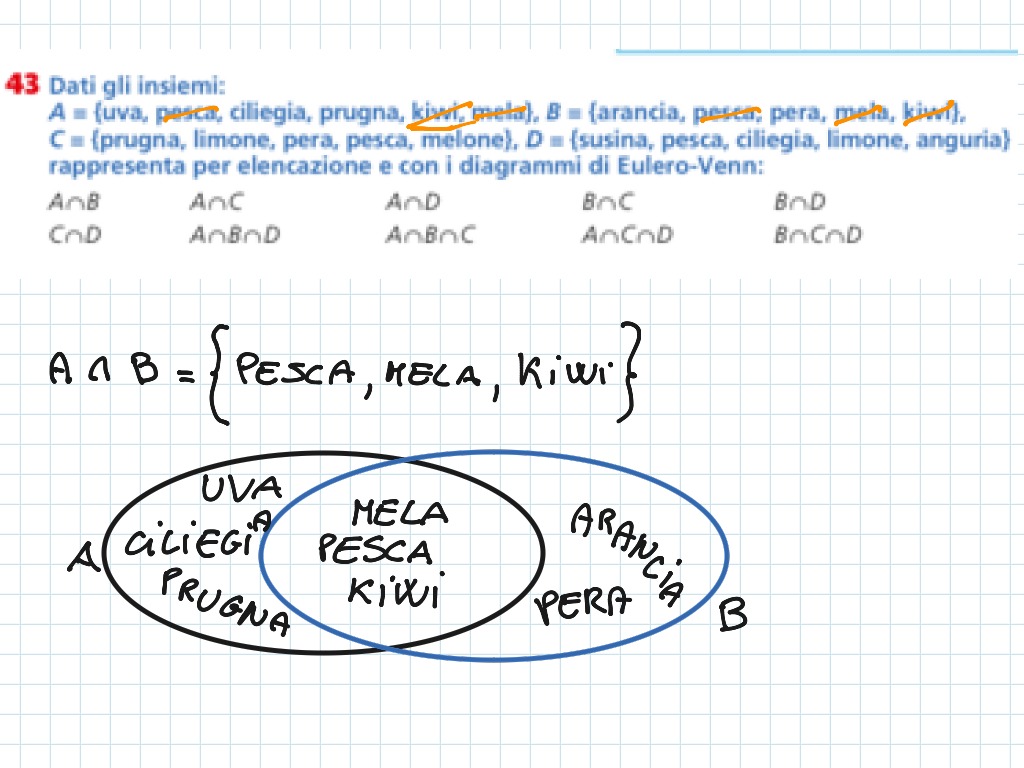
Consiglio per gli studenti: Quando risolvi un esercizio, disegna sempre i diagrammi di Venn. Ti aiuteranno a capire meglio la situazione e a individuare la soluzione.
3. Risolvere gli Esercizi: Un Approccio Sistematico
La pratica è fondamentale per padroneggiare la teoria degli insiemi. Ecco un approccio sistematico per affrontare gli esercizi:
- Leggi attentamente il testo: Assicurati di aver compreso esattamente cosa ti viene chiesto. Identifica gli insiemi coinvolti e le relazioni tra di loro.
- Disegna i diagrammi di Venn: Rappresenta graficamente gli insiemi e le loro relazioni.
- Traduci il problema in linguaggio matematico: Esprimi le informazioni date nel testo utilizzando i simboli degli insiemi (∈, ⊆, ∪, ∩).
- Applica le proprietà degli insiemi: Utilizza le proprietà dell'unione, dell'intersezione, del complemento, ecc., per semplificare l'espressione e trovare la soluzione.
- Verifica la soluzione: Controlla se la soluzione ottenuta soddisfa le condizioni del problema.
Consiglio per gli insegnanti: Proponete esercizi di difficoltà crescente, partendo da esempi semplici e concreti, per poi passare a problemi più complessi e astratti. Incoraggiate gli studenti a spiegare il loro ragionamento e a giustificare le loro risposte.

4. Esercizi e Verifiche: Come Prepararsi al Meglio
Per prepararsi al meglio alle verifiche, è fondamentale svolgere molti esercizi di vario tipo. Cerca online esercizi svolti e verifiche tipo. Molti siti web offrono materiale didattico gratuito per il primo anno del Liceo Scientifico, inclusi file PDF con verifiche sugli insiemi e le relative soluzioni.
Dove trovare verifiche con soluzioni (PDF):
- Cerca su Google: "Verifica insiemi prima liceo scientifico pdf con soluzioni"
- Controlla i siti web delle scuole superiori o dei professori di matematica.
- Utilizza piattaforme di e-learning dedicate alla matematica.
Consiglio per gli studenti: Non limitarti a copiare le soluzioni. Cerca di capire il ragionamento che c'è dietro ogni passaggio. Se hai difficoltà, chiedi aiuto al tuo insegnante o a un compagno di classe.

5. Strategie per Superare l'Ansia da Verifica
L'ansia da verifica è un problema comune, ma esistono strategie efficaci per gestirla:
- Preparati adeguatamente: Più ti senti preparato, meno sarai ansioso.
- Dormi bene la notte prima della verifica: Il riposo è fondamentale per la concentrazione e la memoria.
- Fai esercizi di respirazione: La respirazione profonda può aiutarti a calmare i nervi.
- Visualizza il successo: Immagina di affrontare la verifica con calma e di risolvere correttamente gli esercizi.
- Non focalizzarti sull'errore: Se sbagli un esercizio, non demoralizzarti. Concentrati sul prossimo.
Consiglio per i genitori: Incoraggiate i vostri figli a studiare con metodo e a non procrastinare. Offrite il vostro supporto e create un ambiente di studio positivo e rilassato.
Affrontare le Difficoltà con Fiducia
La matematica, e in particolare la teoria degli insiemi, può sembrare ostica all'inizio, ma con il giusto approccio e un po' di impegno, tutti possono superare le difficoltà. Ricorda che l'importante è non arrendersi mai e affrontare ogni sfida con fiducia e determinazione. La comprensione degli insiemi è una base fondamentale per molti altri argomenti della matematica, quindi dedicare tempo e sforzo a questo argomento ripaga ampiamente nel lungo termine.

Spero che questo articolo ti sia stato utile. In bocca al lupo per la tua verifica!
Riferimenti:
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students' learning. In F. K. Lester Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 371-404). Information Age Publishing.